1.06 Quiz Sinusoidal Graphs Vertical Shift
Onlines
Apr 01, 2025 · 6 min read
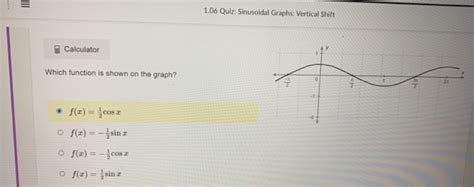
Table of Contents
- 1.06 Quiz Sinusoidal Graphs Vertical Shift
- Table of Contents
- 1.06 Quiz: Mastering Sinusoidal Graphs and Vertical Shifts
- What are Sinusoidal Graphs?
- Understanding Vertical Shifts (D)
- Identifying Vertical Shifts from Equations
- Identifying Vertical Shifts from Graphs
- The Impact of Vertical Shifts on Key Features
- Solving Problems Involving Vertical Shifts
- Advanced Applications and Considerations
- Quiz Preparation Strategies
- Latest Posts
- Latest Posts
- Related Post
1.06 Quiz: Mastering Sinusoidal Graphs and Vertical Shifts
Understanding sinusoidal graphs, specifically their vertical shifts, is crucial for anyone studying trigonometry or pre-calculus. This comprehensive guide will break down the concepts, providing you with the tools and knowledge to confidently tackle any quiz on sinusoidal graphs, including the challenging vertical shift component. We'll go beyond simply understanding the mechanics and delve into the why behind the transformations, ensuring a solid grasp of the underlying principles.
What are Sinusoidal Graphs?
Sinusoidal graphs are graphical representations of sine and cosine functions. These functions are fundamental in trigonometry and describe cyclical or periodic phenomena. Think of things like sound waves, the movement of a pendulum, or even the tides – all exhibit patterns that can be modeled using sinusoidal functions. The basic form of these functions is:
- y = A sin(Bx - C) + D
- y = A cos(Bx - C) + D
Where:
- A represents the amplitude: This determines the height of the wave from the midline to the peak (or trough). A larger A means a taller wave.
- B affects the period: The period is the length of one complete cycle of the wave. The period is calculated as 2π/B. A larger B means a shorter period (more compressed wave).
- C represents the phase shift (horizontal shift): This shifts the graph horizontally to the left or right. A positive C shifts the graph to the right, and a negative C shifts it to the left.
- D represents the vertical shift: This moves the entire graph up or down. A positive D shifts the graph upward, and a negative D shifts it downward.
Understanding Vertical Shifts (D)
The vertical shift, represented by 'D' in the equations above, is arguably one of the most straightforward, yet crucial, transformations of a sinusoidal graph. It literally shifts the entire graph vertically along the y-axis. A positive value of D shifts the graph upwards, and a negative value shifts it downwards.
Imagine you have the basic sine graph, y = sin(x). Now, let's add a vertical shift:
- y = sin(x) + 2: This graph will be identical to y = sin(x), but shifted two units upwards. The midline of the graph, which is normally at y = 0, will now be at y = 2.
- y = sin(x) - 1: This graph will be shifted one unit downwards. The midline will now be at y = -1.
The vertical shift doesn't affect the amplitude or the period of the wave; it only changes its vertical position. This is a key point to remember when analyzing and graphing sinusoidal functions.
Identifying Vertical Shifts from Equations
Identifying the vertical shift from a given equation is simple: just look for the constant term added or subtracted outside of the sine or cosine function. This constant is your 'D' value, directly indicating the vertical shift.
Examples:
- y = 3sin(2x) + 5: The vertical shift is +5. The graph is shifted 5 units upwards.
- y = -2cos(x/2) - 4: The vertical shift is -4. The graph is shifted 4 units downwards.
- y = sin(x - π/4): There's no vertical shift here (D = 0). The graph is only phase-shifted.
Identifying Vertical Shifts from Graphs
Identifying the vertical shift from a graph involves finding the midline of the wave. The midline is the horizontal line that runs exactly halfway between the peak and the trough of the wave. The y-coordinate of this midline represents the vertical shift.
Steps to find the vertical shift from a graph:
- Identify the peak (highest point) and the trough (lowest point) of the wave.
- Find the y-coordinate of the peak and the y-coordinate of the trough.
- Calculate the average of these two y-coordinates: (peak y-coordinate + trough y-coordinate) / 2. This average is the y-coordinate of the midline.
- The y-coordinate of the midline is your vertical shift (D).
The Impact of Vertical Shifts on Key Features
While the vertical shift doesn't alter the amplitude or period, it does change the maximum and minimum values of the function.
- Maximum Value: The maximum value of the function becomes A + D.
- Minimum Value: The minimum value of the function becomes -A + D.
Understanding these changes is crucial for accurately sketching and interpreting sinusoidal graphs.
Solving Problems Involving Vertical Shifts
Let's work through some example problems to solidify your understanding of vertical shifts in sinusoidal graphs:
Problem 1:
Sketch the graph of y = 2cos(x) + 1. Identify the amplitude, period, and vertical shift.
Solution:
- Amplitude (A): 2
- Period: 2π/B = 2π/1 = 2π (Since B = 1)
- Vertical Shift (D): 1 (The graph is shifted one unit upwards.)
To sketch the graph, start with the basic cosine graph. Then, stretch it vertically by a factor of 2 (amplitude), and finally, shift the entire graph one unit upwards.
Problem 2:
A sinusoidal wave has a maximum value of 7 and a minimum value of -1. What is the amplitude and the vertical shift?
Solution:
- Find the amplitude: The amplitude is half the difference between the maximum and minimum values: (7 - (-1))/2 = 4.
- Find the midline: The midline is the average of the maximum and minimum values: (7 + (-1))/2 = 3.
- The vertical shift: The midline represents the vertical shift, which is 3.
Therefore, the amplitude is 4, and the vertical shift is 3.
Problem 3:
The graph of y = sin(x) is transformed to y = 3sin(2x) - 2. Describe the transformations.
Solution:
- Amplitude: The amplitude is increased from 1 to 3.
- Period: The period is reduced from 2π to π (2π/2 = π).
- Vertical Shift: The graph is shifted 2 units downwards.
Advanced Applications and Considerations
Understanding vertical shifts is fundamental to modeling real-world phenomena. For instance, in modeling the tides, the vertical shift would represent the average tide level, while the amplitude would represent the tidal range. Similarly, in modeling sound waves, the vertical shift could represent a baseline pressure, and the amplitude would reflect the loudness.
By mastering the concept of vertical shifts, you gain a deeper understanding of the flexibility and power of sinusoidal functions in representing various cyclical processes. Remember to practice regularly, working through different problems and scenarios to build confidence and proficiency. Focus on connecting the abstract mathematical concepts with their visual representations on the graph.
Quiz Preparation Strategies
To prepare effectively for your quiz on sinusoidal graphs and vertical shifts, consider the following strategies:
- Review fundamental trigonometric identities. A solid understanding of sine and cosine functions is essential.
- Practice graphing various sinusoidal functions with different amplitudes, periods, phase shifts, and vertical shifts. Use graph paper or online graphing tools to visualize these transformations.
- Work through plenty of practice problems. Focus on problems that combine different transformations.
- Understand the relationship between the equation of a sinusoidal function and its graph. Be able to identify the key features (amplitude, period, phase shift, vertical shift) from both the equation and the graph.
- Identify common mistakes. Many students struggle with correctly interpreting the signs of the vertical shift or confusing it with the amplitude. Pay close attention to these details.
By following these strategies and diligently practicing, you'll be well-prepared to confidently tackle your 1.06 quiz on sinusoidal graphs, especially those involving vertical shifts. Remember to break down complex problems into smaller, manageable steps, and don't be afraid to seek help if needed. Good luck!
Latest Posts
Latest Posts
-
Which Of The Following Is The Best Example Of Cogeneration
Apr 04, 2025
-
What Are Two More Purposes Of The Violent Incident Log
Apr 04, 2025
-
Kumon Answer Book Pdf Level D
Apr 04, 2025
-
Select The Social Media Site That Is An Idea Sharing Website
Apr 04, 2025
-
7 7 Skills Practice Scale Drawings And Models
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 1.06 Quiz Sinusoidal Graphs Vertical Shift . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
