1 1 2 14 7 4 10 31
Onlines
May 09, 2025 · 5 min read
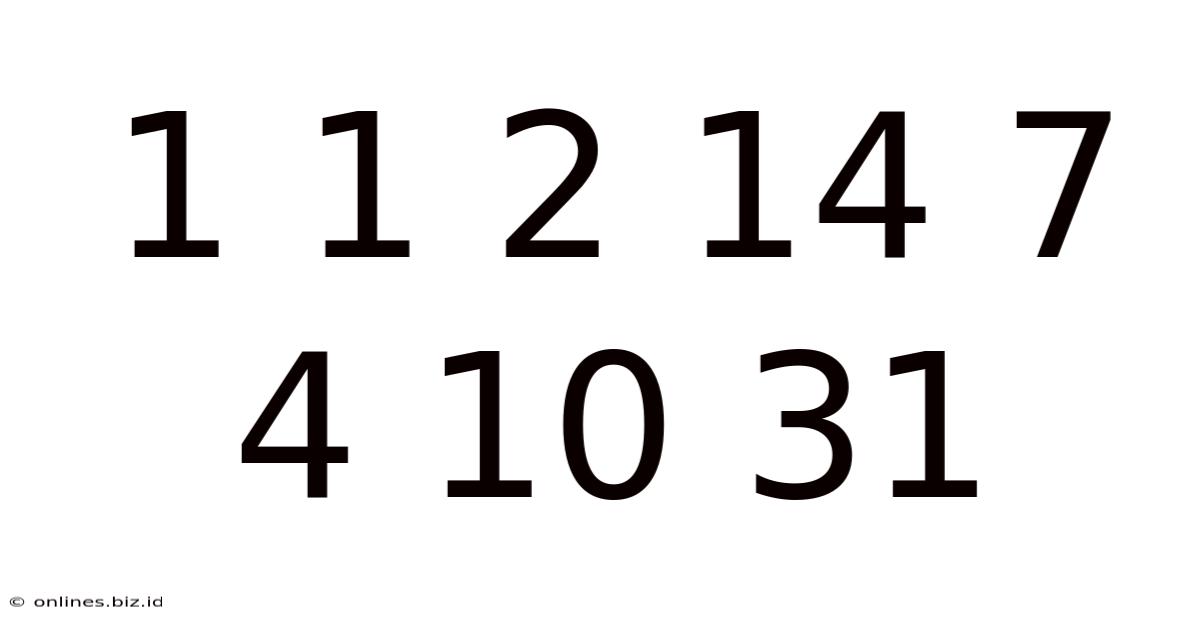
Table of Contents
- 1 1 2 14 7 4 10 31
- Table of Contents
- Unraveling the Enigma: The Sequence 1 1 2 14 7 4 10 31
- The Allure of Pattern Recognition: Why This Sequence Matters
- Potential Approaches to Deciphering the Sequence
- 1. Differences and Finite Differences
- 2. Exploring Relationships Between Consecutive Terms
- 3. Considering Recursive Relationships
- 4. Investigating Prime Numbers and Factorization
- 5. Searching for Hidden Patterns and Codes
- The Importance of Context and Additional Information
- Conclusion: A Journey of Exploration and Discovery
- Latest Posts
- Related Post
Unraveling the Enigma: The Sequence 1 1 2 14 7 4 10 31
The seemingly innocuous sequence 1, 1, 2, 14, 7, 4, 10, 31... presents a captivating challenge. At first glance, it appears random, defying immediate recognition of a pattern. However, with careful analysis and a blend of mathematical reasoning and creative problem-solving, we can explore various potential underlying structures and generate hypotheses about its construction. This article will delve into several approaches to deciphering this intriguing sequence, highlighting the fascinating interplay between logic, mathematics, and the creative process of pattern recognition.
The Allure of Pattern Recognition: Why This Sequence Matters
The human brain is wired to seek patterns. We find comfort and understanding in identifying order within apparent chaos. Sequences like 1 1 2 14 7 4 10 31 tap into this inherent human tendency. Understanding the principles behind such sequences isn't merely an academic exercise; it enhances critical thinking skills, strengthens logical reasoning, and provides insight into the abstract nature of mathematics. Furthermore, the process of unraveling these patterns mirrors the problem-solving techniques employed in various fields, from cryptography to data analysis.
Potential Approaches to Deciphering the Sequence
Several avenues exist to investigate the sequence 1 1 2 14 7 4 10 31. Let's explore some key approaches:
1. Differences and Finite Differences
A common technique in analyzing sequences is to examine the differences between consecutive terms. Let's calculate the first-order differences:
- 1 - 1 = 0
- 2 - 1 = 1
- 14 - 2 = 12
- 7 - 14 = -7
- 4 - 7 = -3
- 10 - 4 = 6
- 31 - 10 = 21
The first-order differences (0, 1, 12, -7, -3, 6, 21) don't immediately reveal a clear pattern. Let's try calculating the second-order differences:
- 1 - 0 = 1
- 12 - 1 = 11
- -7 - 12 = -19
- -3 - (-7) = 4
- 6 - (-3) = 9
- 21 - 6 = 15
Again, no obvious pattern emerges. Continuing with higher-order differences might yield results, but the lack of a clear pattern at this stage suggests that this method might not be the most fruitful approach for this specific sequence.
2. Exploring Relationships Between Consecutive Terms
Let's investigate potential relationships between adjacent terms in the sequence. We can explore various mathematical operations: addition, subtraction, multiplication, division, and combinations thereof. For example:
- Addition: Adding consecutive terms doesn't produce a consistent pattern.
- Subtraction: Subtracting consecutive terms, as we did in the finite differences method, didn't yield a clear pattern.
- Multiplication: Multiplying consecutive terms also fails to reveal a consistent pattern.
- Division: Dividing consecutive terms isn't revealing either.
The lack of clear relationships using basic arithmetic operations indicates that a more complex underlying structure might govern the sequence.
3. Considering Recursive Relationships
Recursive sequences define each term based on preceding terms. Let's explore whether a recursive relationship could explain the sequence 1 1 2 14 7 4 10 31. We could hypothesize various recursive formulas and test their validity against the given sequence. Finding a recursive formula that accurately generates the sequence would be a significant breakthrough. However, without more terms in the sequence, this approach remains speculative.
4. Investigating Prime Numbers and Factorization
Prime numbers and their properties often play a role in mathematical sequences. Let's examine the prime factorization of each term in the sequence:
- 1 = 1
- 1 = 1
- 2 = 2
- 14 = 2 x 7
- 7 = 7
- 4 = 2 x 2
- 10 = 2 x 5
- 31 = 31
While this doesn't immediately show a clear pattern, investigating the distribution and relationships between the prime factors could potentially unveil hidden connections. Further analysis might involve exploring the sum of prime factors, the number of prime factors, or other properties related to prime factorization.
5. Searching for Hidden Patterns and Codes
Sometimes, a sequence might be based on a concealed code or a less obvious mathematical rule. This could involve:
- Number systems: Could the sequence be representing numbers in a different number system (binary, ternary, etc.)? Converting the numbers to other bases might reveal a hidden pattern.
- Modular arithmetic: Exploring modular arithmetic, which involves operations with remainders, could potentially uncover a hidden relationship.
- Geometric progressions or other mathematical series: While the sequence doesn't seem to fit typical geometric or arithmetic progressions, exploring variations or combinations of these series could be insightful.
- Cipher or Code: Could the sequence be a code, where the numbers represent letters or symbols according to a specific cipher? This is less likely without a key or additional context.
The Importance of Context and Additional Information
The difficulty in deciphering the sequence 1 1 2 14 7 4 10 31 highlights the importance of context. Without additional information about the origin or intended meaning of the sequence, finding a definitive solution remains challenging. More terms in the sequence would dramatically improve our ability to identify patterns and develop plausible models. Knowing the context in which this sequence appeared—whether it's part of a larger problem, a puzzle, or a mathematical riddle—would provide valuable clues.
Conclusion: A Journey of Exploration and Discovery
The exploration of the sequence 1 1 2 14 7 4 10 31 is a testament to the beauty and complexity of mathematical patterns. While a definitive solution might elude us without further information, the process of investigating potential underlying structures provides valuable practice in problem-solving, logical reasoning, and creative thinking. The sequence serves as a reminder that the search for patterns is an ongoing process of exploration and discovery, and sometimes, the journey itself is as rewarding as the destination. The pursuit of understanding this sequence illustrates the power of mathematical inquiry and the human capacity for finding order in apparent randomness. Further investigation, perhaps incorporating more advanced mathematical tools or additional data points, may ultimately lead to a compelling explanation of this intriguing numerical puzzle.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 1 2 14 7 4 10 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.