100 Times My Number Is 12.6 More Than 5000
Onlines
May 09, 2025 · 4 min read
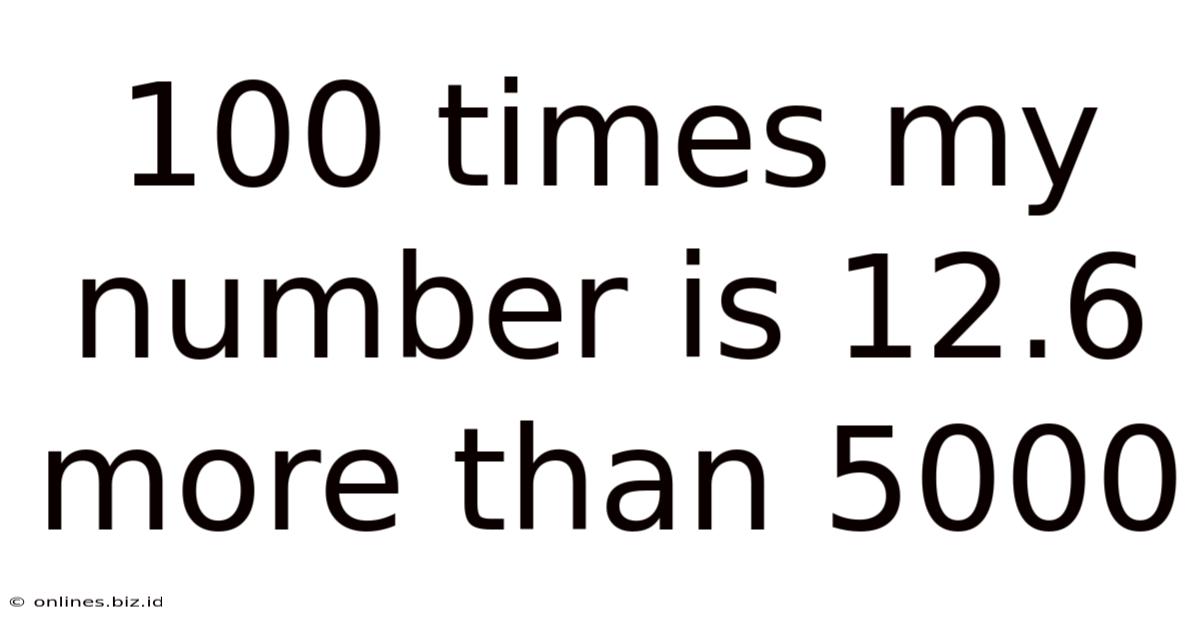
Table of Contents
100 Times My Number is 12.6 More Than 5000: Solving the Equation and Exploring Related Concepts
This article delves into the solution of the mathematical problem: "100 times my number is 12.6 more than 5000," exploring the underlying algebraic concepts, demonstrating the solution process step-by-step, and extending the discussion to encompass related mathematical principles. We'll examine how to approach similar problems, the importance of understanding algebraic manipulation, and practical applications of such equations in various fields.
Understanding the Problem
The statement "100 times my number is 12.6 more than 5000" can be translated into a mathematical equation. Let's represent "my number" with the variable 'x'. The equation then becomes:
100x = 5000 + 12.6
This equation states that 100 multiplied by an unknown number (x) is equal to 5000 plus 12.6. Our goal is to solve for 'x', determining the value of this unknown number.
Solving the Equation: A Step-by-Step Guide
Solving this equation involves using basic algebraic principles. Here's the step-by-step process:
-
Simplify the right-hand side: First, we simplify the right-hand side of the equation by adding 5000 and 12.6:
5000 + 12.6 = 5012.6
The equation now becomes:
100x = 5012.6
-
Isolate the variable: To isolate 'x', we need to eliminate the coefficient 100. We do this by dividing both sides of the equation by 100:
100x / 100 = 5012.6 / 100
-
Solve for x: Performing the division, we find the value of x:
x = 50.126
Therefore, the solution to the problem is that "my number" is 50.126.
Verification of the Solution
It's always a good practice to verify the solution by substituting the calculated value of 'x' back into the original equation:
100 * 50.126 = 5012.6
5000 + 12.6 = 5012.6
Since both sides of the equation are equal, our solution (x = 50.126) is correct.
Expanding on Algebraic Concepts
This simple problem showcases fundamental algebraic concepts:
-
Variables: The use of 'x' to represent the unknown number is a crucial aspect of algebra. Variables allow us to represent unknown quantities and manipulate them within equations.
-
Equations: An equation shows the equality between two expressions. Solving an equation involves finding the value(s) of the variable(s) that make the equation true.
-
Solving Equations: This involves applying inverse operations (like division to counteract multiplication) to isolate the variable and find its value.
Practical Applications of Algebraic Equations
Algebraic equations, even simple ones like the one we solved, have widespread applications in various fields:
-
Science: Scientific models often involve equations to describe relationships between different variables. For example, calculating the speed of an object, determining the concentration of a solution, or modeling population growth all involve solving equations.
-
Engineering: Engineers rely heavily on equations to design structures, analyze systems, and optimize processes. From designing bridges to programming software, equations are fundamental.
-
Finance: Financial calculations, such as calculating interest, determining loan repayments, or analyzing investments, often require solving equations.
-
Economics: Economic models use equations to describe relationships between supply and demand, inflation and unemployment, and other economic variables.
-
Everyday Life: Many everyday situations can be modeled using simple equations. For example, calculating the total cost of groceries, determining the distance traveled, or planning a budget can all benefit from understanding and applying equations.
Solving Similar Problems: Variations and Extensions
Let's consider some variations of the original problem to further illustrate the application of these principles:
Problem 1: 25 times my number is 7.5 less than 1000.
This translates to the equation: 25x = 1000 - 7.5. Solving this equation similarly to the original one, we find x = 39.7.
Problem 2: My number multiplied by 150 is 25 more than 10000.
This translates to: 150x = 10000 + 25. Solving this, we get x ≈ 67.1667.
Importance of Precision and Significant Figures
Note that in the above examples, we maintain a consistent level of precision in our calculations. Depending on the context, the number of significant figures you use will vary. In many real-world applications, especially those related to measurement, it's crucial to consider significant figures to accurately represent the results and avoid misleading interpretations.
Beyond Basic Algebra: Further Exploration
While this problem focuses on basic algebraic manipulation, more complex scenarios may involve:
-
Systems of Equations: Problems may involve multiple equations with multiple unknowns, requiring techniques like substitution or elimination to solve.
-
Quadratic Equations: Equations involving squared terms (x²) require different techniques like factoring, the quadratic formula, or completing the square to solve.
-
Higher-Order Equations: Equations with higher powers of x require more advanced algebraic methods.
-
Inequalities: Instead of equalities, problems may involve inequalities (>, <, ≥, ≤), requiring different approaches to find the solution set.
Conclusion
The seemingly simple problem, "100 times my number is 12.6 more than 5000," serves as a gateway to understanding fundamental algebraic principles. Mastering the ability to translate word problems into mathematical equations and solve them is crucial not just for academic success but also for tackling real-world challenges in numerous fields. By understanding the underlying concepts and practicing solving various types of equations, you develop a powerful toolset for problem-solving and critical thinking. Remember to always verify your solutions and consider the implications of precision and significant figures when working with numerical data. The more you practice, the more confident and proficient you'll become in applying these valuable mathematical skills.
Latest Posts
Latest Posts
-
The Accreditation Program Of Ahima Is Concerned With
May 10, 2025
-
Were English Mariners Of The Elizabethan Era
May 10, 2025
-
A Status Byte For A Program Change Message Contains The
May 10, 2025
-
Which Expression Is Equivalent To Mc009 1 Jpg
May 10, 2025
-
For Internal Cooling Reciprocating Aircraft Engines Are Especially Dependent On
May 10, 2025
Related Post
Thank you for visiting our website which covers about 100 Times My Number Is 12.6 More Than 5000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.