14 1 Practice Three Dimensional Figures And Cross Sections Answers
Onlines
Apr 02, 2025 · 6 min read
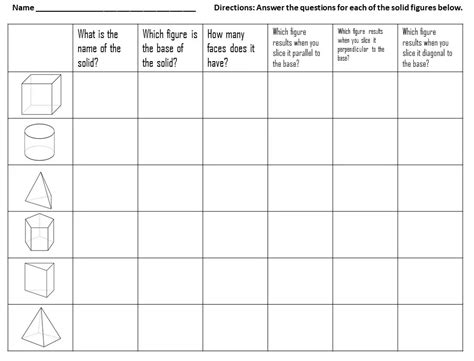
Table of Contents
14.1 Practice: Three-Dimensional Figures and Cross Sections - Answers and Explanations
This comprehensive guide provides detailed answers and explanations for the problems typically found in a 14.1 practice section covering three-dimensional figures and cross sections in geometry. We'll explore various shapes, their properties, and how to visualize and describe their cross sections. This resource aims to solidify your understanding of this crucial geometric concept, helping you ace your next test and build a strong foundation for future mathematical endeavors.
Understanding Three-Dimensional Figures
Before diving into cross sections, let's refresh our understanding of the fundamental three-dimensional figures. These are shapes that exist in three dimensions – length, width, and height. Common examples include:
-
Prisms: Polyhedra with two parallel congruent bases connected by lateral faces that are parallelograms. Examples include rectangular prisms (like boxes), triangular prisms, and hexagonal prisms. The key is the parallel and congruent bases.
-
Pyramids: Polyhedra with a polygonal base and triangular lateral faces that meet at a single point called the apex. Like prisms, pyramids are classified by the shape of their base (e.g., square pyramid, triangular pyramid).
-
Cylinders: Three-dimensional figures with two parallel congruent circular bases connected by a curved lateral surface.
-
Cones: Three-dimensional figures with a circular base and a curved lateral surface that tapers to a single point called the apex.
-
Spheres: Three-dimensional figures with all points equidistant from a central point called the center.
Key Properties to Remember
When working with three-dimensional figures, remember these key properties:
- Faces: The flat surfaces of a three-dimensional figure.
- Edges: The line segments where two faces meet.
- Vertices: The points where three or more edges meet.
- Base(s): The face(s) used to classify the figure (e.g., the square base of a square pyramid).
Cross Sections: Slicing Through Shapes
A cross section is the two-dimensional shape formed by the intersection of a plane and a three-dimensional figure. Imagine slicing through a shape with a perfectly straight knife; the resulting cut surface is the cross section. The shape and orientation of the plane significantly impact the shape of the cross section.
Types of Cross Sections
The type of cross section you obtain depends on both the three-dimensional figure and the angle at which you slice it. Here are some possibilities:
-
Parallel to the base: If the plane is parallel to the base of a prism or cylinder, the cross section will be congruent to the base. For a pyramid or cone, it will be similar to the base but smaller.
-
Perpendicular to the base: This often results in a polygon related to the shape of the lateral faces. For example, slicing a triangular prism perpendicular to its base will produce a rectangle.
-
Oblique cuts: These create more complex cross sections that are not as easily predictable. They depend heavily on the angle of the plane relative to the faces of the three-dimensional figure.
Example Problems and Solutions (14.1 Practice)
Let's walk through some typical problems found in a 14.1 practice section on three-dimensional figures and cross sections. Remember that these are examples, and your specific problems might vary.
Problem 1: Describe the cross section formed when a plane intersects a rectangular prism parallel to its base.
Solution: The cross section will be a rectangle congruent to the base of the rectangular prism. Since the plane is parallel to the base, it slices through the prism, creating a rectangle identical in shape and size to the top and bottom faces.
Problem 2: A square pyramid is intersected by a plane parallel to its base. Describe the shape of the cross section.
Solution: The cross section will be a square. While smaller than the base, it will be similar in shape, maintaining its square proportions.
Problem 3: What is the shape of the cross section formed when a plane intersects a cylinder perpendicular to its bases?
Solution: The cross section will be a rectangle. The plane cuts through the curved lateral surface, creating a rectangle with a width equal to the diameter of the base and a length equal to the height of the cylinder.
Problem 4: Describe the possible cross sections of a sphere.
Solution: The cross section of a sphere will always be a circle, regardless of the orientation of the plane. This is because any plane slicing through a sphere will create a circular intersection.
Problem 5: A triangular prism is cut by a plane that is perpendicular to its rectangular faces but not parallel to its triangular bases. What shape is the resulting cross section?
Solution: The resulting cross section will be a trapezoid. The angle of the cut plane relative to the triangular bases will determine the specific dimensions of the trapezoid, but it will always be a trapezoid due to the geometry of the prism.
Problem 6: A cone is intersected by a plane parallel to its base. Describe the cross section.
Solution: The cross section will be a circle. The plane will create a circular intersection, similar in shape to the base but smaller in size.
Problem 7: A cube is intersected by a plane that cuts through four of its vertices, forming a cross section. What are the possible shapes of this cross section?
Solution: Depending on which four vertices the plane intersects, the cross section could be a square, a rectangle, or a rhombus. This illustrates the diversity of cross sections attainable depending on the intersecting plane's position.
Problem 8: Imagine a hexagonal prism. Describe the cross section formed by a plane that is perpendicular to one of the hexagonal bases.
Solution: The cross section will be a hexagon congruent to the base of the hexagonal prism. This is analogous to slicing a rectangular prism parallel to its base.
Problem 9: Consider a cylinder. A plane passes through the cylinder at an angle, not parallel nor perpendicular to the bases. Describe the possible shape(s) of the cross section.
Solution: The cross section will be an ellipse. The orientation and angle of the plane will determine the specific dimensions of the ellipse.
Problem 10: A square pyramid is cut by a plane that intersects its apex and two opposite vertices of the base. What is the shape of the cross section?
Solution: The cross section will be an isosceles triangle. The plane cuts through three vertices, resulting in a triangle where two sides are equal due to the symmetry of the square pyramid.
Advanced Concepts and Further Exploration
This practice covers the fundamentals of three-dimensional figures and cross sections. Further exploration might include:
-
Cavalieri's Principle: This principle helps compare the volumes of solids with similar cross sections.
-
Volume calculations of irregular shapes using cross sections: More advanced problems might involve calculating volumes by integrating cross-sectional areas.
-
Exploring cross sections of more complex three-dimensional shapes: Consider shapes that combine different geometric elements (e.g., a cylinder with a cone on top).
-
Using cross-sectional analysis in real-world applications: From architecture to engineering to medical imaging, understanding cross sections is essential.
By carefully considering the orientation of the plane and the properties of the three-dimensional figure, you can accurately predict the shape of the cross section. Remember to visualize the slice and use your understanding of two-dimensional shapes to describe the resulting cross section accurately. Consistent practice and visualization will solidify your understanding of this important geometric concept. Remember to always consider the orientation of the slicing plane in relation to the key features (bases, vertices, edges) of the three-dimensional figure. This will aid you in accurately predicting the shape of the cross section. Good luck with your studies!
Latest Posts
Latest Posts
-
Which Is Not Recommended When Giving Feedback
Apr 03, 2025
-
A Simple Elevator Ride Can Teach
Apr 03, 2025
-
Penelope 1 Of 1 Muestra Sus Fotos A Mi
Apr 03, 2025
-
What Property Of Oil Makes It Float On Water
Apr 03, 2025
-
Betraying The Trust Of Your Audience Is
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 14 1 Practice Three Dimensional Figures And Cross Sections Answers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
