2-1 Additional Practice Slope Intercept Form
Onlines
Apr 01, 2025 · 8 min read
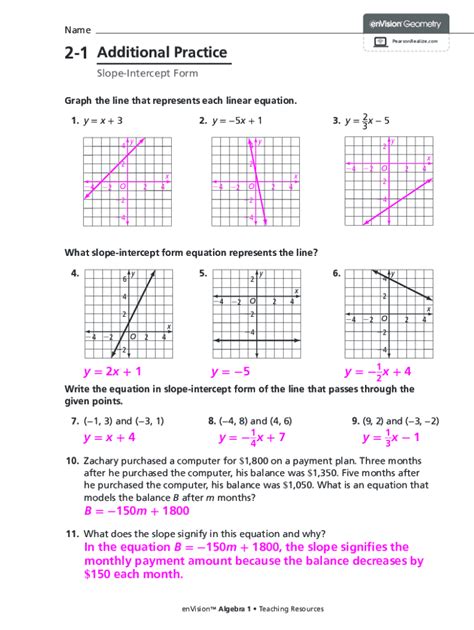
Table of Contents
Mastering the Slope-Intercept Form: 2-1 Additional Practice
The slope-intercept form, y = mx + b, is a cornerstone of algebra. Understanding it thoroughly unlocks a world of possibilities in graphing linear equations, solving real-world problems, and building a strong foundation for more advanced mathematical concepts. While the initial learning curve might seem steep, consistent practice is key to mastering this fundamental form. This comprehensive guide provides ample additional practice problems, focusing on various levels of difficulty and incorporating diverse problem-solving techniques.
Understanding the Fundamentals: A Quick Recap
Before diving into the practice problems, let's briefly revisit the key components of the slope-intercept form:
- y: Represents the dependent variable; its value depends on the value of x.
- x: Represents the independent variable; its value is chosen freely.
- m: Represents the slope of the line. The slope describes the steepness and direction of the line. A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0).
Practice Problems: Level 1 - Basic Application
These problems focus on directly applying the slope-intercept form given the slope and y-intercept.
Problem 1: Write the equation of a line with a slope of 2 and a y-intercept of 5.
Solution: Substitute m = 2 and b = 5 into the equation y = mx + b. The equation is y = 2x + 5.
Problem 2: A line has a slope of -3 and crosses the y-axis at (0, -1). What is its equation?
Solution: Here, m = -3 and b = -1. The equation is y = -3x - 1.
Problem 3: Graph the line represented by the equation y = 1/2x + 3.
Solution: The y-intercept is 3, so plot the point (0, 3). The slope is 1/2, meaning for every 2 units increase in x, y increases by 1 unit. Starting from (0, 3), move 2 units to the right and 1 unit up to find another point (2, 4). Draw a line through these points to graph the equation.
Problem 4: What is the slope and y-intercept of the line represented by the equation y = -4x + 7?
Solution: The slope (m) is -4 and the y-intercept (b) is 7.
Problem 5: Write the equation of a horizontal line passing through the point (3, 2).
Solution: A horizontal line has a slope of 0. The equation is y = 2. (The y-coordinate remains constant).
Practice Problems: Level 2 - Finding Slope and Y-Intercept
These problems require you to determine the slope and y-intercept from given information, often using two points on the line.
Problem 6: Find the equation of the line that passes through the points (1, 3) and (3, 7).
Solution: First, calculate the slope: m = (7 - 3) / (3 - 1) = 2. Then, use the point-slope form (y - y1 = m(x - x1)) with one of the points (e.g., (1, 3)): y - 3 = 2(x - 1). Simplify to get y = 2x + 1.
Problem 7: A line passes through points (-2, 4) and (2, 0). What is its equation in slope-intercept form?
Solution: Calculate the slope: m = (0 - 4) / (2 - (-2)) = -1. Use the point-slope form with (2, 0): y - 0 = -1(x - 2). Simplify to get y = -x + 2.
Problem 8: Determine the slope and y-intercept of the line passing through (0, -5) and (2, 1).
Solution: The point (0, -5) gives us the y-intercept directly (b = -5). Calculate the slope using (0, -5) and (2, 1): m = (1 - (-5)) / (2 - 0) = 3. The equation is y = 3x - 5.
Problem 9: The line passes through (-1, 2) and (1, 6). What is its equation?
Solution: Calculate the slope: m = (6 - 2) / (1 - (-1)) = 2. Using point-slope form with (-1, 2): y - 2 = 2(x + 1). Simplify to get y = 2x + 4.
Problem 10: A line is parallel to y = 3x + 1 and passes through (1, 4). Find its equation.
Solution: Parallel lines have the same slope. The slope is 3. Use point-slope form with (1, 4): y - 4 = 3(x - 1). Simplify to get y = 3x + 1. Notice that this is the same as the original line because it also passes through (1,4). However, any other point different than the original line would yield a parallel line.
Practice Problems: Level 3 - Word Problems and Real-World Applications
These problems incorporate the slope-intercept form into real-world scenarios, requiring you to translate word problems into mathematical equations.
Problem 11: A taxi charges a $3 initial fare plus $2 per mile. Write an equation representing the total cost (y) as a function of the number of miles (x).
Solution: The initial fare is the y-intercept (b = 3). The cost per mile is the slope (m = 2). The equation is y = 2x + 3.
Problem 12: A plant grows 1 inch per week. It is currently 5 inches tall. Write an equation showing the plant's height (y) after x weeks.
Solution: The growth rate is the slope (m = 1). The initial height is the y-intercept (b = 5). The equation is y = x + 5.
Problem 13: A candle is 10 inches tall and burns at a rate of 0.5 inches per hour. Write an equation showing the candle's height (y) after x hours.
Solution: The initial height is the y-intercept (b = 10). The burning rate is the negative slope (m = -0.5). The equation is y = -0.5x + 10.
Problem 14: A phone plan charges $20 per month plus $0.10 per minute. Write an equation for the monthly cost (y) based on the number of minutes used (x).
Solution: The monthly base fee is the y-intercept (b = 20). The cost per minute is the slope (m = 0.10). The equation is y = 0.10x + 20.
Problem 15: A car rental company charges $30 per day plus $0.25 per mile. If you spent $80 on a rental, and drove 200 miles, was the charge correct? Explain.
Solution: The equation representing the total cost (y) is y = 0.25x + 30. where x represents the number of miles. Substitute x = 200: y = 0.25(200) + 30 = 80. The charge was correct.
Practice Problems: Level 4 - Challenging Applications
These problems involve more complex scenarios and require a deeper understanding of the slope-intercept form and related concepts.
Problem 16: Two lines are perpendicular. One line has an equation of y = 2x + 5. If the other line passes through (2, 1), what is its equation?
Solution: Perpendicular lines have slopes that are negative reciprocals of each other. The slope of the given line is 2, so the slope of the perpendicular line is -1/2. Use point-slope form with (2, 1): y - 1 = -1/2(x - 2). Simplify to get y = -1/2x + 2.
Problem 17: Find the equation of the line that is parallel to y = -x + 3 and passes through the midpoint of (1, 5) and (5, 1).
Solution: First, find the midpoint: ((1+5)/2, (5+1)/2) = (3, 3). Parallel lines have the same slope, which is -1 in this case. Use point-slope form with (3, 3): y - 3 = -1(x - 3). Simplify to get y = -x + 6.
Problem 18: A line passes through (4, 6) and is perpendicular to the line connecting (1, 2) and (3, 8). What is its equation?
Solution: Find the slope of the line connecting (1, 2) and (3, 8): m = (8 - 2) / (3 - 1) = 3. The slope of the perpendicular line is -1/3. Use point-slope form with (4, 6): y - 6 = -1/3(x - 4). Simplify to get y = -1/3x + 22/3.
Problem 19: A line has a y-intercept of 4 and makes an angle of 45 degrees with the positive x-axis. Find its equation.
Solution: A 45-degree angle corresponds to a slope of 1 (tan(45°) = 1). The y-intercept is 4. Therefore, the equation is y = x + 4.
Problem 20: The sum of the x-intercept and the y-intercept of a line is 8, and the line passes through (1, 2). Find its equation.
Solution: Let the x-intercept be a and the y-intercept be b. Then a + b = 8. The line passes through (0, b) and (a, 0). The slope is m = -b/a. Using point-slope form with (1, 2): y - 2 = -b/a(x - 1). Substitute a = 8 - b: y - 2 = -b/(8 - b)(x - 1). This equation and a + b = 8 are a system of equations that are difficult to solve analytically. However, you can plug in the point (1,2) into the equation y=mx+b where m is the slope and b is the y intercept. Then you can solve for the values of m and b and thereby get the equation of the line.
By working through these practice problems, you will significantly enhance your understanding and proficiency in using the slope-intercept form of linear equations. Remember that consistent practice and a methodical approach are crucial to mastering this fundamental algebraic concept. Don't hesitate to revisit the fundamental concepts and work through the problems multiple times to solidify your understanding. Good luck!
Latest Posts
Latest Posts
-
Unit 7 Right Triangles And Trigonometry Homework 4 Answers Key
Apr 02, 2025
-
Ap English Language And Composition Section 1 Answer Key
Apr 02, 2025
-
Cloze Ing In On Science Organisms And Environments Answers
Apr 02, 2025
-
Rates Of Chemical Reactions Lab Report
Apr 02, 2025
-
Development Of A Human Fetus Lab Answer Key Pdf
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 2-1 Additional Practice Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
