28.52 Is What Percent Of 77.5
Onlines
May 12, 2025 · 5 min read
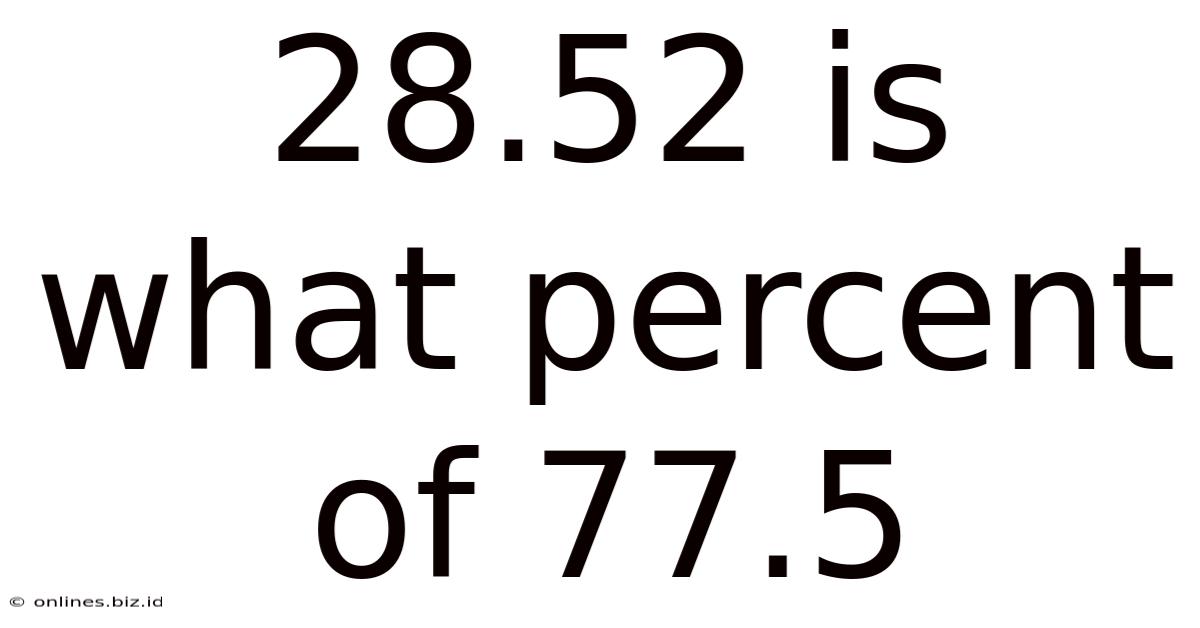
Table of Contents
28.52 is What Percent of 77.5? A Comprehensive Guide to Percentage Calculations
Determining what percentage one number represents of another is a fundamental mathematical concept with wide-ranging applications in various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of calculating percentages, specifically addressing the question: "28.52 is what percent of 77.5?" We'll not only solve this specific problem but also explore the underlying principles and provide you with the tools to tackle similar percentage calculations with ease.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this basic definition is crucial for performing percentage calculations.
Calculating Percentages: The Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
Where:
- Part: This represents the number you want to express as a percentage of the whole. In our example, the part is 28.52.
- Whole: This represents the total or the entire amount. In our example, the whole is 77.5.
- Percentage: This is the result of the calculation, expressed as a percentage.
Step-by-Step Calculation: 28.52 is What Percent of 77.5?
Let's apply the formula to solve our specific problem:
-
Identify the Part and the Whole:
- Part = 28.52
- Whole = 77.5
-
Substitute into the Formula:
- (28.52 / 77.5) * 100% = Percentage
-
Perform the Division:
- 28.52 / 77.5 ≈ 0.36826
-
Multiply by 100%:
- 0.36826 * 100% ≈ 36.826%
-
Round to the Desired Precision:
- Depending on the context, you may need to round the result. Rounding to two decimal places, we get 36.83%.
Therefore, 28.52 is approximately 36.83% of 77.5.
Practical Applications of Percentage Calculations
Percentage calculations are incredibly versatile and find applications in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for making informed financial decisions.
-
Statistics: Percentages are used extensively in data analysis to represent proportions, frequencies, and changes in data sets. They are essential for interpreting statistical findings and making meaningful comparisons.
-
Science: Percentage calculations are used in various scientific fields, including chemistry (concentration of solutions), physics (efficiency of processes), and biology (population growth).
-
Everyday Life: From calculating tips at restaurants to understanding sale prices in stores, percentages are woven into the fabric of our daily lives. Knowing how to calculate percentages empowers us to make more informed decisions and navigate everyday situations more effectively.
Advanced Percentage Calculations: Variations and Challenges
While the basic formula provides a solid foundation, some percentage calculations can present additional challenges:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole using a slightly modified formula: Whole = (Part / Percentage) * 100
-
Finding the Part: If you know the percentage and the whole, you can calculate the part using: Part = (Percentage/100) * Whole
-
Percentage Change: Calculating the percentage increase or decrease between two numbers involves finding the difference between the two numbers, dividing it by the original number, and then multiplying by 100%. The formula is: ((New Value - Old Value) / Old Value) * 100%
-
Compounding Percentages: When dealing with percentages that accumulate over time, such as compound interest, the calculations become more complex and require iterative methods or specific formulas.
Tips and Tricks for Accurate Percentage Calculations
-
Use a Calculator: For complex calculations or to avoid errors, using a calculator is highly recommended. Most calculators have a percentage function that simplifies the process.
-
Double-Check Your Work: Always double-check your calculations to ensure accuracy, particularly when dealing with financial matters or scientific data. Small errors in percentage calculations can have significant consequences.
-
Understand the Context: Pay close attention to the context of the problem. Clearly identify the part and the whole before applying the formula. Misinterpreting the context can lead to incorrect results.
-
Practice Regularly: The more you practice percentage calculations, the more comfortable and proficient you will become. Work through various examples, including those with different levels of difficulty.
Expanding Your Knowledge: Further Exploration of Percentage Concepts
To further enhance your understanding of percentage calculations, consider exploring these related topics:
-
Ratio and Proportion: Percentages are closely related to ratios and proportions. Understanding these concepts can provide a deeper insight into the mathematical underpinnings of percentage calculations.
-
Decimal and Fraction Conversions: Fluency in converting between decimals, fractions, and percentages is essential for efficient percentage calculations. Mastering these conversions will significantly streamline the process.
-
Advanced Statistical Concepts: For a more in-depth understanding of percentages in data analysis, exploring advanced statistical concepts such as standard deviation, variance, and confidence intervals is beneficial.
-
Financial Modeling: Learning how to apply percentage calculations within financial models can provide invaluable skills for careers in finance and investment.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is a valuable skill applicable across various aspects of life, from personal finance and everyday decisions to professional fields like finance, statistics, and science. Understanding the fundamental formula, practicing regularly, and applying the tips outlined above will equip you to tackle percentage problems with confidence and accuracy. Remember, the key to success lies in a solid grasp of the underlying concepts and consistent practice. By diligently applying these principles, you'll confidently navigate the world of percentages and leverage their power in your daily life and professional endeavors. The example problem, "28.52 is what percent of 77.5?", serves as a practical illustration of these concepts, demonstrating the straightforward yet powerful application of percentage calculations in various contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 28.52 Is What Percent Of 77.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.