6-5 Study Guide And Intervention Rhombi And Squares
Onlines
Apr 02, 2025 · 6 min read
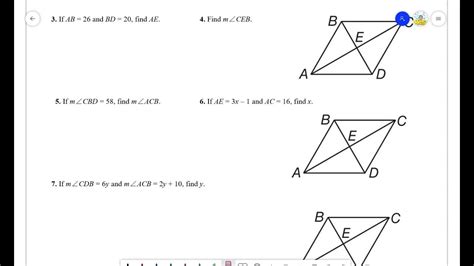
Table of Contents
6-5 Study Guide and Intervention: Rhombi and Squares
This comprehensive study guide delves into the geometric properties of rhombi and squares, crucial concepts within geometry and often covered in high school mathematics curricula. We'll explore their definitions, theorems, and how they relate to each other, providing a robust understanding to ace your exams and solidify your geometric knowledge.
Understanding Quadrilaterals: A Foundation
Before diving into rhombi and squares specifically, let's establish a foundational understanding of quadrilaterals. A quadrilateral is any polygon with four sides. Several special types of quadrilaterals exist, each possessing unique properties. These include parallelograms, rectangles, rhombi, squares, trapezoids, and kites. Understanding the hierarchical relationship between these shapes is key to grasping the specific attributes of rhombi and squares.
Parallelograms: The Parent Shape
A parallelogram is a quadrilateral where both pairs of opposite sides are parallel. This fundamental property leads to several other characteristics:
- Opposite sides are congruent: The lengths of opposite sides are equal.
- Opposite angles are congruent: The measures of opposite angles are equal.
- Consecutive angles are supplementary: The sum of the measures of any two consecutive angles is 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at their midpoints.
Rhombi: Properties and Theorems
A rhombus is a special type of parallelogram. It inherits all the properties of a parallelogram but adds a crucial defining characteristic: all four sides are congruent. This added property leads to additional unique attributes:
- Diagonals are perpendicular: The diagonals of a rhombus intersect at a 90-degree angle.
- Diagonals bisect the angles: Each diagonal bisects a pair of opposite angles.
Theorem 1: If a parallelogram is a rhombus, then its diagonals are perpendicular bisectors of each other.
Theorem 2: If a quadrilateral is a parallelogram with perpendicular diagonals, then it is a rhombus.
Theorem 3: If a quadrilateral is a parallelogram with congruent diagonals, then it is a rectangle. Note that a rhombus with congruent diagonals is a square (explained in detail below).
Theorem 4: If a quadrilateral has four congruent sides, it is a rhombus.
Let's illustrate these properties with an example. Consider rhombus ABCD, where AB = BC = CD = DA. The diagonals AC and BD intersect at point E. Then:
- AE = EC and BE = ED (diagonals bisect each other).
- ∠AEB = ∠BEC = ∠CED = ∠DEA = 90° (diagonals are perpendicular).
- ∠DAB = ∠DCB and ∠ABC = ∠CDA (opposite angles are congruent).
- ∠DAE = ∠BAE = ∠BCE = ∠DCE and ∠ABE = ∠CBE = ∠ADE = ∠CDE (diagonals bisect angles).
Squares: The Most Specialized Quadrilateral
A square is the most specialized type of quadrilateral. It possesses all the properties of a parallelogram, a rectangle, and a rhombus. Therefore, a square is:
- A parallelogram with four congruent sides and four right angles.
- A rectangle with four congruent sides.
- A rhombus with four right angles.
The defining properties of a square are:
- Four congruent sides: All four sides are of equal length.
- Four right angles: All four angles measure 90 degrees.
- Diagonals are congruent and perpendicular bisectors: The diagonals are equal in length, intersect at right angles, and bisect each other.
- Diagonals bisect the angles: Each diagonal bisects a pair of opposite angles, resulting in four 45-degree angles.
Theorem 5: If a quadrilateral is a rhombus and a rectangle, then it is a square.
Theorem 6: If a quadrilateral has four right angles and four congruent sides, then it is a square.
Problem Solving: Applying the Properties
Let's solidify our understanding through example problems:
Problem 1: Given rhombus ABCD with AB = 6 cm and ∠ABC = 120°. Find the length of the diagonal AC.
Solution: In a rhombus, the diagonals bisect the angles. Therefore, ∠ABE = 60°. Since AB = 6 cm and ∠ABE = 60°, triangle ABE is a 30-60-90 triangle. Using trigonometric ratios, we can find AE: AE = AB * cos(60°) = 6 * (1/2) = 3 cm. Since the diagonals bisect each other, AC = 2 * AE = 2 * 3 = 6 cm.
Problem 2: Prove that the diagonals of a square are perpendicular bisectors of each other.
Solution: Let ABCD be a square. Since a square is a parallelogram, its diagonals bisect each other. Let the diagonals intersect at point E. Consider triangles ABE and CBE. AB = CB (sides of a square), BE = BE (common side), and ∠ABE = ∠CBE = 45° (diagonals bisect angles). Therefore, triangles ABE and CBE are congruent by SAS (Side-Angle-Side). This implies AE = CE and ∠AEB = ∠CEB. Since ∠AEB + ∠CEB = 180° (angles on a straight line), we have 2∠AEB = 180°, which means ∠AEB = 90°. Thus, the diagonals are perpendicular.
Problem 3: A quadrilateral has diagonals that are perpendicular bisectors of each other. Is it necessarily a rhombus? Is it necessarily a square?
Solution: The quadrilateral is necessarily a rhombus because the perpendicular bisecting diagonals are a defining characteristic of a rhombus. However, it is not necessarily a square. A rhombus with diagonals of different lengths is not a square; a square has congruent diagonals.
Advanced Concepts and Applications
Beyond the fundamental properties, understanding rhombi and squares extends to more advanced geometric concepts:
-
Area Calculations: The area of a rhombus is given by (1/2)d1d2, where d1 and d2 are the lengths of the diagonals. The area of a square is simply s², where s is the side length.
-
Coordinate Geometry: Applying coordinate geometry principles allows calculating the lengths of sides and diagonals, finding the slopes of lines to prove perpendicularity, and determining the coordinates of intersection points.
-
Trigonometry: Trigonometric functions are invaluable when dealing with angle measures and side lengths in problems involving rhombi and squares.
Real-World Applications
Rhombi and squares, though seemingly abstract geometric concepts, appear in numerous real-world applications:
-
Architecture and Design: Square and rhombus shapes are frequently used in building structures, tiling patterns, and architectural designs for their aesthetic appeal and structural stability.
-
Engineering: These shapes play a vital role in engineering design, particularly in structural engineering where their stability and symmetry are advantageous.
-
Art and Design: The visual symmetry and geometric properties of rhombi and squares are frequently exploited in art, design, and graphic works.
Conclusion: Mastering Rhombi and Squares
This comprehensive guide provides a thorough understanding of rhombi and squares, encompassing their definitions, theorems, problem-solving techniques, and real-world applications. By mastering these concepts, you'll not only excel in your geometry studies but also develop a deeper appreciation for the elegance and utility of geometric shapes in various fields. Remember to practice diligently by solving various problems to reinforce your understanding and build confidence in tackling more complex geometric challenges. Continuous practice and application are crucial for achieving mastery in this area of mathematics.
Latest Posts
Latest Posts
-
Using Fitness Evaluations To Determine Fitness Levels Is Important To
Apr 03, 2025
-
A Medical Transport Helicopter Is Incoming
Apr 03, 2025
-
3 11 Quiz Cry The Beloved Country H
Apr 03, 2025
-
Nail Creams Are Barrier Products Because They
Apr 03, 2025
-
Interchanges Take The Place Of Intersections On Expressways
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 6-5 Study Guide And Intervention Rhombi And Squares . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
