8 2 Skills Practice The Pythagorean Theorem And Its Converse
Onlines
Apr 04, 2025 · 5 min read
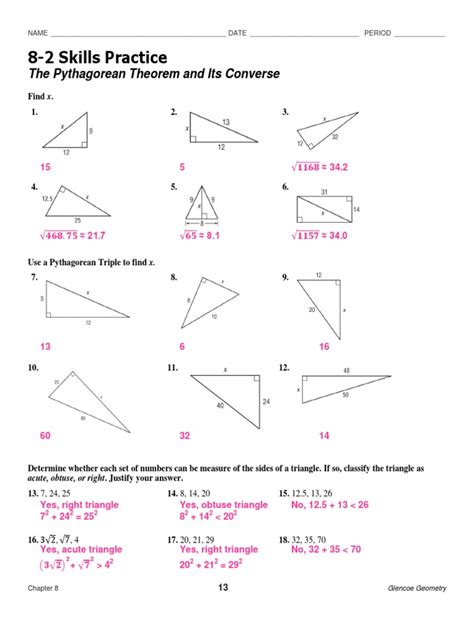
Table of Contents
8+2 Skills to Practice the Pythagorean Theorem and its Converse
The Pythagorean Theorem is a cornerstone of geometry, and mastering it unlocks a world of problem-solving possibilities. While the theorem itself is relatively straightforward – a² + b² = c² (where a and b are the legs of a right-angled triangle and c is the hypotenuse) – true understanding requires practical application and a nuanced grasp of its converse. This article outlines eight core skills and two bonus skills that, when practiced diligently, will solidify your understanding and enable you to confidently tackle a wide range of problems involving the Pythagorean Theorem and its converse.
Core Skills: Mastering the Pythagorean Theorem
These eight skills form the bedrock of your Pythagorean Theorem expertise. Practice each one thoroughly to build a strong foundation.
1. Identifying Right-Angled Triangles
Before you even think about applying the theorem, you need to confidently identify a right-angled triangle. This means being able to spot the presence of a 90-degree angle, often indicated by a small square in diagrams. Practice recognizing right-angled triangles in various orientations and within more complex shapes. This seemingly simple step is crucial – applying the Pythagorean Theorem to a non-right triangle will lead to incorrect results.
2. Understanding the Theorem's Components
Clearly distinguish between the hypotenuse (the side opposite the right angle, always the longest side) and the legs (the two shorter sides). Mislabeling these will directly impact your calculations. Regularly practice labeling the sides of right-angled triangles to reinforce this fundamental understanding. Use different notations (a, b, c; x, y, z; etc.) to become comfortable with varied representations.
3. Calculating the Hypotenuse
This is the most common application of the theorem: finding the length of the hypotenuse when the lengths of the legs are known. Work through numerous examples with varying values for a and b. Pay attention to units of measurement and ensure your answer is in the correct units (e.g., cm, m, inches). Include examples with both whole numbers and decimals to build proficiency.
Example: If a = 3 cm and b = 4 cm, then c² = 3² + 4² = 9 + 16 = 25, so c = √25 = 5 cm.
4. Calculating a Leg
This involves rearranging the formula to solve for either 'a' or 'b' when you know the hypotenuse and one leg. This requires algebraic manipulation, a skill crucial for many mathematical applications. Practice solving for both 'a' and 'b' using various values for 'c' and the other leg.
Example: If c = 10 cm and a = 6 cm, then b² = c² - a² = 10² - 6² = 100 - 36 = 64, so b = √64 = 8 cm.
5. Working with Decimals and Fractions
The Pythagorean Theorem applies to triangles with sides of any length. Practice problems involving decimals and fractions to build your comfort with these types of calculations. Remember to use a calculator accurately and round your answers appropriately according to the context of the problem.
6. Solving Word Problems
Translate real-world scenarios into mathematical problems involving right-angled triangles. This skill tests your ability to apply the theorem in practical contexts. Look for keywords like "distance," "height," "length," and "diagonal" to identify right-angled triangles within descriptions.
Example: A ladder 10 meters long leans against a wall, reaching 8 meters up the wall. How far is the base of the ladder from the wall?
7. Understanding Pythagorean Triples
Pythagorean triples are sets of three whole numbers that satisfy the Pythagorean Theorem (e.g., 3, 4, 5; 5, 12, 13). Recognizing these triples can significantly speed up calculations. Memorizing a few common triples will save you time and increase your efficiency.
8. Applying the Theorem in More Complex Shapes
The Pythagorean Theorem isn't limited to simple triangles. Practice using it to find lengths within more complex shapes, such as rectangles, squares, and other polygons. Often, you'll need to break down the shape into right-angled triangles to apply the theorem effectively. This skill requires spatial reasoning and problem-solving abilities.
Bonus Skills: Mastering the Converse of the Pythagorean Theorem
These two skills delve into the converse of the theorem, expanding your problem-solving capabilities.
1. Understanding the Converse
The converse of the Pythagorean Theorem states that if the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right-angled triangle. This allows you to determine whether a triangle is right-angled based solely on its side lengths.
2. Applying the Converse to Determine Right Angles
Use the converse to determine if a given triangle is a right-angled triangle without directly measuring angles. This is incredibly useful when working with triangles where angle measurements are not provided, or in real-world situations where direct angle measurement is impractical.
Example: A triangle has sides of length 6, 8, and 10. Since 10² (100) = 6² + 8² (36 + 64 = 100), the triangle is a right-angled triangle.
Practice Makes Perfect: Tips for Improvement
- Consistent Practice: Regular practice is key. Work through a variety of problems each day, gradually increasing the difficulty.
- Use Different Resources: Utilize textbooks, online resources, and practice worksheets to expose yourself to various problem types.
- Seek Feedback: If possible, have someone review your work to identify areas for improvement.
- Visual Aids: Draw diagrams to help visualize the triangles and their dimensions.
- Real-World Applications: Try to apply the theorem to real-world problems to enhance understanding and retention.
- Master Algebraic Manipulation: A strong understanding of algebra is essential for effectively using and rearranging the Pythagorean Theorem's formula.
By mastering these eight core skills and two bonus skills, you'll develop a deep understanding of the Pythagorean Theorem and its converse, allowing you to tackle a vast range of geometrical problems with confidence and accuracy. Remember, consistent practice is the key to success in mastering any mathematical concept. So, grab a pencil and paper and start practicing!
Latest Posts
Latest Posts
-
A Nurse Is Preparing To Participate In An Interdisciplinary Conference
Apr 04, 2025
-
All Of The Following Movements Cause Carpal Tunnel Syndrome Except
Apr 04, 2025
-
Compared To Commercial Operations Managed Services Have The Advantage Of
Apr 04, 2025
-
An Aerial View Of The Layout Of Each Room
Apr 04, 2025
-
Farmers Need To Make Many Decisions
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 8 2 Skills Practice The Pythagorean Theorem And Its Converse . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
