Calculate The Length B To Two Decimal Places
Onlines
Apr 06, 2025 · 5 min read
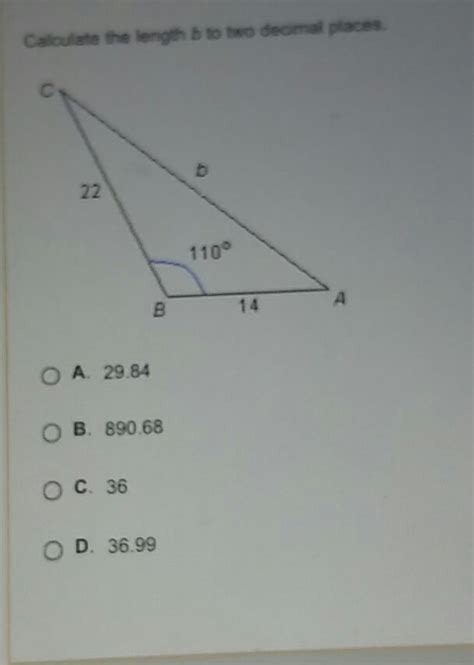
Table of Contents
Calculate the Length 'b' to Two Decimal Places: A Comprehensive Guide
Determining the length of an unknown side in various geometric shapes is a fundamental concept in mathematics and numerous real-world applications. This article provides a comprehensive guide on how to calculate the length 'b' to two decimal places, covering various scenarios and employing different mathematical techniques. We will explore several methods, from basic geometry to more advanced trigonometric approaches, emphasizing practical application and step-by-step solutions. Understanding these methods empowers you to solve a wide range of problems involving length calculations.
Understanding the Context: What Information Do We Need?
Before we delve into the calculation methods, it's crucial to understand that calculating 'b' necessitates possessing specific information about the geometric shape involved. The required data varies depending on the shape:
1. Right-Angled Triangles:
For right-angled triangles, we can use the Pythagorean theorem or trigonometric functions (sine, cosine, tangent). To use the Pythagorean theorem (a² + b² = c²), we need the lengths of at least two sides. If we know the hypotenuse (c) and one leg (a), we can solve for b. Trigonometric functions require the length of one side and the measure of one of the acute angles.
2. Other Triangles:
Calculating 'b' in other triangles (isosceles, equilateral, scalene) requires different approaches. We might need to use the Law of Sines, the Law of Cosines, or a combination of both, depending on the known information. Knowing at least three elements of the triangle (sides or angles) is typically necessary.
3. Other Geometric Shapes:
For other shapes like quadrilaterals, circles, or complex polygons, the calculation of 'b' depends on the specific shape and the given dimensions. This often involves breaking down the shape into simpler components, such as triangles, to apply known geometric principles.
Calculating 'b' in Right-Angled Triangles
Right-angled triangles are the foundation of many length calculations. Let's explore two key approaches:
1. Using the Pythagorean Theorem:
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs). The formula is:
a² + b² = c²
Where:
- a and b are the lengths of the legs.
- c is the length of the hypotenuse.
To solve for 'b', we rearrange the formula:
b = √(c² - a²)
Example: If a = 3 cm and c = 5 cm, then:
b = √(5² - 3²) = √(25 - 9) = √16 = 4 cm
Therefore, b = 4.00 cm (to two decimal places).
2. Using Trigonometric Functions:
Trigonometric functions (sine, cosine, tangent) relate the angles and sides of a right-angled triangle.
- sin(θ) = opposite/hypotenuse = b/c
- cos(θ) = adjacent/hypotenuse = a/c
- tan(θ) = opposite/adjacent = b/a
Where θ is an acute angle in the triangle.
To solve for 'b', we use the appropriate function depending on the known information.
Example 1: If a = 4 cm and θ = 30°, then:
tan(30°) = b/4 b = 4 * tan(30°) ≈ 4 * 0.577 ≈ 2.31 cm
Therefore, b ≈ 2.31 cm (to two decimal places).
Example 2: If c = 10 cm and θ = 45°, then:
sin(45°) = b/10 b = 10 * sin(45°) ≈ 10 * 0.707 ≈ 7.07 cm
Therefore, b ≈ 7.07 cm (to two decimal places).
Calculating 'b' in Other Triangles
For triangles that are not right-angled, we use the Law of Sines and the Law of Cosines.
1. The Law of Sines:
The Law of Sines states that the ratio of the length of a side to the sine of the opposite angle is constant for all three sides of any triangle. The formula is:
a/sin(A) = b/sin(B) = c/sin(C)
Where:
- a, b, c are the lengths of the sides.
- A, B, C are the angles opposite to sides a, b, c respectively.
To solve for 'b', we rearrange the formula:
b = a * sin(B) / sin(A)
This requires knowing at least one side and its opposite angle, along with another angle.
2. The Law of Cosines:
The Law of Cosines is a generalization of the Pythagorean theorem for any triangle. It relates the lengths of the sides to the cosine of one of the angles. The formula is:
c² = a² + b² - 2ab * cos(C)
To solve for 'b', we need to rearrange this equation, which can be quite complex and often results in a quadratic equation. Solving quadratic equations might require using the quadratic formula.
This requires knowing the lengths of two sides and the angle between them.
Calculating 'b' in Other Geometric Shapes
Calculating 'b' in other shapes often involves a combination of techniques. Consider these examples:
1. Circles:
Calculating a specific length 'b' in a circle might involve using the circle's radius, circumference, or area, depending on the context. For instance, finding the length of a chord requires knowing the radius and the distance from the chord to the center.
2. Parallelograms:
In parallelograms, opposite sides are equal in length. Therefore, if you know the length of one side, you automatically know the length of its opposite side.
3. Trapezoids:
Solving for 'b' in a trapezoid requires using the properties of trapezoids, often involving breaking the trapezoid down into simpler shapes (e.g., triangles and rectangles) to apply known geometric formulas.
4. Regular Polygons:
Calculating the side length ('b') of a regular polygon requires knowledge of the polygon's apothem (distance from the center to the midpoint of a side) and the number of sides. Using trigonometry, you can determine the side length.
Practical Applications and Real-World Examples
The ability to calculate 'b' (or any unknown length) is essential in many fields:
- Engineering: Calculating distances, stresses, and strains in structures.
- Surveying: Determining distances and land areas.
- Architecture: Designing buildings and structures.
- Computer Graphics: Creating realistic 3D models.
- Navigation: Calculating distances and bearings.
Conclusion: Mastering Length Calculations
Calculating the length 'b' to two decimal places, while seemingly a simple task, requires a thorough understanding of geometry and trigonometry. This article provides a solid foundation for tackling various problems involving length calculations. Remember to carefully identify the geometric shape, determine the known information, and select the appropriate formula or method. Practice is key to mastering these skills and applying them effectively in diverse real-world contexts. By carefully following the steps and examples outlined here, you can confidently solve a wide range of problems involving the calculation of unknown lengths. Remember to always double-check your calculations and use appropriate units for your final answer. Consistent practice will refine your ability to solve these problems accurately and efficiently.
Latest Posts
Latest Posts
-
Unit 7 Polynomials And Factoring Homework 7 Answer Key
Apr 06, 2025
-
The Love Hypothesis Chapter 16 Adam Pov Read Online Free
Apr 06, 2025
-
Which Of The Following Is True Of Integral Membrane Proteins
Apr 06, 2025
-
101 Animal Word Search Answer Key
Apr 06, 2025
-
If A Patient Demonstrates Irritability And Verbal Profanity
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Calculate The Length B To Two Decimal Places . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
