Classify Each Histogram Using The Appropriate Descriptions
Onlines
Apr 02, 2025 · 6 min read
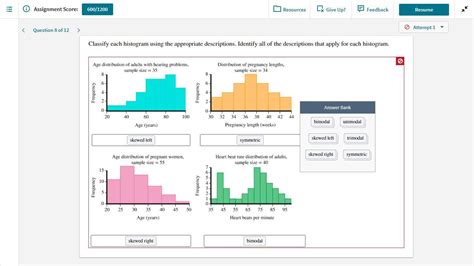
Table of Contents
Classify Each Histogram Using the Appropriate Descriptions
Histograms are powerful visual tools used to represent the distribution of numerical data. Understanding how to classify histograms based on their shape and characteristics is crucial for data analysis and interpretation. This comprehensive guide will explore various histogram classifications, providing detailed descriptions and examples to help you confidently interpret these visual representations of data. We'll delve into the nuances of each type, highlighting key features and the implications they hold for the underlying data.
Understanding the Basics of Histograms
Before diving into classification, let's briefly review the fundamentals of histograms. A histogram is a bar graph-like representation where the x-axis represents the range of values (bins or intervals) and the y-axis represents the frequency or count of data points falling within each bin. Unlike bar charts, the bars in a histogram are contiguous, indicating a continuous data range. The width of each bar typically represents the size of the bin, and the height corresponds to the frequency.
Classifying Histograms by Shape
Histograms are primarily classified based on their visual shape, which reveals important insights about the underlying data distribution. The most common classifications include:
1. Symmetrical Histograms
A symmetrical histogram exhibits a mirror-like symmetry around its central point (mean, median, and mode are approximately equal). The left and right halves of the histogram are roughly identical. This indicates a balanced distribution where data points are evenly spread around the central tendency.
Characteristics:
- Equal Mean, Median, and Mode: The measures of central tendency are approximately equal.
- Bell-shaped Curve: Often resembles a bell-shaped curve, although not necessarily a perfect normal distribution.
- Data is evenly distributed around the center.
Example: A histogram showing the heights of a large, randomly selected population might exhibit approximate symmetry.
2. Skewed Histograms
Skewed histograms are asymmetrical, with a longer tail extending to one side. The direction of the skew indicates the direction of the longer tail.
a) Positively Skewed Histograms (Right-Skewed)
A positively skewed histogram (also known as right-skewed) has a longer tail extending to the right. The mean is typically greater than the median, and the median is greater than the mode. This suggests the presence of a few high values that pull the mean towards the right.
Characteristics:
- Longer right tail: The tail extends further to the right.
- Mean > Median > Mode: The mean is greater than the median, which is greater than the mode.
- Indicates the presence of outliers or extreme values on the higher end.
Example: Income distribution often exhibits positive skew due to the presence of high-income earners.
b) Negatively Skewed Histograms (Left-Skewed)
A negatively skewed histogram (also known as left-skewed) has a longer tail extending to the left. The mean is typically less than the median, and the median is less than the mode. This suggests the presence of a few low values pulling the mean towards the left.
Characteristics:
- Longer left tail: The tail extends further to the left.
- Mean < Median < Mode: The mean is less than the median, which is less than the mode.
- Indicates the presence of outliers or extreme values on the lower end.
Example: Exam scores on an extremely difficult test might show a negative skew due to a concentration of low scores.
3. Unimodal Histograms
A unimodal histogram has a single peak (mode). This indicates a concentration of data points around a single central value.
Characteristics:
- One distinct peak: Only one prominent mode is present.
- Data is clustered around a single central value.
Example: The heights of adult women within a specific age range often exhibit a unimodal distribution.
4. Bimodal Histograms
A bimodal histogram possesses two distinct peaks (modes). This suggests the presence of two distinct groups or subgroups within the data. The data might represent two different populations combined or a data set with two different processes contributing to the observations.
Characteristics:
- Two distinct peaks: Two prominent modes are clearly visible.
- May indicate the presence of two underlying populations or sub-populations.
Example: The heights of both adult men and women combined would likely show a bimodal distribution.
5. Multimodal Histograms
Multimodal histograms have more than two peaks (modes). Similar to bimodal histograms, this often indicates that the data might consist of several distinct subgroups or different underlying distributions.
Characteristics:
- Three or more distinct peaks: Several prominent modes are visible.
- May suggest several underlying populations or processes contributing to the data.
Example: The distribution of ages in a large city might be multimodal, showing peaks for different age groups.
6. Uniform Histograms (Rectangular)
A uniform histogram (also called rectangular) has approximately equal frequencies across all bins. The bars are roughly the same height, indicating that all values within the data range are equally likely.
Characteristics:
- Bars of approximately equal height: The frequencies are nearly consistent across all bins.
- All values within the range are equally likely.
Example: A histogram of randomly generated numbers between 0 and 1 would likely show a uniform distribution.
Interpreting Histogram Shapes: Beyond Simple Classifications
While the above classifications provide a starting point for understanding histogram shapes, it’s crucial to consider the context and potential nuances within the data. For example, a slightly asymmetrical histogram might not definitively fall into the "skewed" category; the degree of asymmetry needs consideration. Similarly, the presence of outliers can significantly influence the shape, potentially masking underlying patterns.
The Importance of Bin Width
The choice of bin width significantly impacts the appearance of a histogram. A smaller bin width might reveal more details but could lead to a more jagged appearance, while a larger bin width might smooth out the details but could hide important features. Therefore, selecting an appropriate bin width is critical for accurate interpretation. Experimenting with different bin widths can provide a more comprehensive understanding of the data distribution.
Beyond Shape: Other Considerations
While shape is the primary basis for classifying histograms, other factors can also influence interpretation:
- Outliers: The presence of outliers (extreme values significantly different from the majority of the data) can distort the overall shape and affect the measures of central tendency.
- Sample Size: The sample size affects the reliability of the histogram. A small sample size might produce a histogram that doesn't accurately reflect the true population distribution.
- Data Type: Understanding whether the data is continuous or discrete is crucial for interpreting the histogram correctly. Continuous data represents values along a continuous scale, while discrete data represents whole numbers or categories.
Conclusion: Mastering Histogram Interpretation
Understanding histogram classifications is a fundamental skill in data analysis. By carefully examining the shape, identifying the presence of skewness, modes, and outliers, and considering the impact of bin width and sample size, you can extract meaningful insights from your data. Remember to always interpret histograms in the context of the underlying data and research question. The ability to accurately classify and interpret histograms will greatly enhance your ability to visualize and understand your data, leading to more informed decisions and a deeper understanding of the patterns and trends within your datasets. Consistent practice and critical thinking are key to mastering this essential data visualization skill.
Latest Posts
Latest Posts
-
Which Of The Following Is True About Interest Groups
Apr 03, 2025
-
Researchers Believe That Mental Recuperation Takes Place During
Apr 03, 2025
-
Ap Physics 1 Unit 7 Progress Check Mcq Part B
Apr 03, 2025
-
Summary Of Chapter 8 Of Animal Farm
Apr 03, 2025
-
Assisted Living Can Be Thought Of As A Combination Of
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Classify Each Histogram Using The Appropriate Descriptions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
