Consider A Binomial Experiment With N 20 And P 0.70
Onlines
Apr 01, 2025 · 6 min read
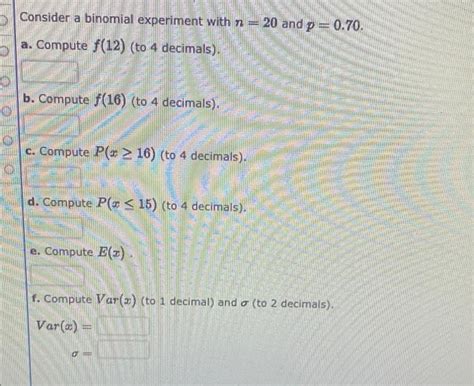
Table of Contents
Delving Deep into a Binomial Experiment: n = 20, p = 0.70
Understanding binomial distributions is crucial in various fields, from statistics and probability to data science and even finance. This comprehensive guide dives deep into a specific binomial experiment with n = 20 (number of trials) and p = 0.70 (probability of success). We'll explore its key characteristics, calculate probabilities, and discuss its practical applications. We'll also touch upon the importance of understanding the assumptions underlying binomial distributions for accurate analysis.
Understanding the Binomial Distribution
A binomial experiment is a statistical experiment that satisfies four key conditions:
- Fixed Number of Trials (n): The experiment consists of a fixed number of independent trials. In our case, n = 20.
- Independent Trials: The outcome of each trial is independent of the outcome of any other trial. The result of one trial doesn't influence the result of subsequent trials.
- Two Possible Outcomes: Each trial has only two possible outcomes: success or failure.
- Constant Probability of Success (p): The probability of success (p) remains constant for each trial. Here, p = 0.70, meaning the probability of success on any single trial is 70%.
The binomial probability formula helps us calculate the probability of getting exactly k successes in n trials:
P(X = k) = (nCk) * p<sup>k</sup> * (1-p)<sup>(n-k)</sup>
Where:
- P(X = k): The probability of getting exactly k successes.
- nCk (or <sub>n</sub>C<sub>k</sub>): The number of combinations of n items taken k at a time (also written as "n choose k"). This is calculated as n! / (k! * (n-k)!).
- p: The probability of success in a single trial (0.70 in our example).
- (1-p): The probability of failure in a single trial (0.30 in our example).
- k: The number of successes we're interested in.
Calculating Probabilities for n = 20 and p = 0.70
Let's apply this formula to calculate several probabilities for our binomial experiment:
Probability of Exactly 14 Successes
Using the formula with k = 14:
P(X = 14) = (20C14) * (0.70)<sup>14</sup> * (0.30)<sup>6</sup>
Calculating the binomial coefficient: 20C14 = 38760
P(X = 14) ≈ 0.1916
Therefore, the probability of getting exactly 14 successes in 20 trials is approximately 19.16%.
Probability of 10 or Fewer Successes
To find P(X ≤ 10), we need to sum the probabilities for X = 0, 1, 2,...10. This can be computationally intensive. Statistical software or online calculators can greatly simplify this process. The result will be a cumulative probability, representing the chance of observing 10 or fewer successes.
Probability of at Least 15 Successes
This involves calculating P(X ≥ 15), which is the sum of P(X = 15) + P(X = 16) + ... + P(X = 20). Again, using software or an online calculator is highly recommended for efficiency.
Probability of Between 12 and 18 Successes (Inclusive)
This requires summing the probabilities from P(X = 12) to P(X = 18). This can be calculated using the formula for each value and adding the results or using a cumulative distribution function (CDF) available in statistical software packages.
Mean, Variance, and Standard Deviation
The binomial distribution has key descriptive statistics that provide insights into its central tendency and spread:
- Mean (μ): The expected number of successes. This is calculated as μ = n * p = 20 * 0.70 = 14.
- Variance (σ²): A measure of the spread or dispersion of the distribution. This is calculated as σ² = n * p * (1-p) = 20 * 0.70 * 0.30 = 4.2.
- Standard Deviation (σ): The square root of the variance, representing the typical deviation from the mean. σ = √(4.2) ≈ 2.05.
These statistics give us a good understanding of the expected outcome and the variability around that expectation.
Using Statistical Software and Online Calculators
Calculating binomial probabilities manually can be tedious, especially for larger values of n. Statistical software packages such as R, Python (with libraries like SciPy), and Excel offer built-in functions to calculate binomial probabilities and related statistics quickly and accurately. Many online calculators are also available for this purpose.
For instance, in R, the dbinom() function calculates the probability mass function (the probability of exactly k successes), while pbinom() calculates the cumulative distribution function.
Applications of Binomial Distribution with n=20, p=0.70
The binomial distribution with these parameters has many practical applications. Consider these examples:
- Quality Control: A manufacturing process produces items with a 70% success rate. Inspecting a batch of 20 items, what's the probability of finding at least 18 acceptable items?
- Medical Trials: A new drug has a 70% success rate in clinical trials. What's the probability that at least 15 out of 20 patients will show improvement?
- Marketing Campaigns: A marketing campaign has a 70% conversion rate. What is the probability of converting at least 12 out of 20 potential customers?
- Election Polling: In a poll of 20 randomly selected voters, each having a 70% chance of voting for a particular candidate, what's the likelihood that at least 16 will vote for that candidate?
Important Considerations and Assumptions
It's crucial to remember that the accuracy of the binomial distribution relies on meeting its underlying assumptions. If these assumptions are violated, the results may not accurately reflect the real-world scenario.
- Independence: If the trials are not independent (e.g., the outcome of one trial influences the next), the binomial distribution may not be appropriate.
- Constant Probability: The probability of success (p) must remain constant across all trials. If the probability changes, alternative statistical models might be necessary.
- Binary Outcomes: The experiment must have only two distinct outcomes (success/failure). If there are multiple outcomes, other probability distributions might be more suitable.
Beyond the Basics: Approximations and Extensions
For large values of n, calculating binomial probabilities can be computationally challenging. In such cases, approximations, such as the normal approximation to the binomial, can be useful. This approximation relies on the central limit theorem and uses the normal distribution to approximate the binomial distribution. The accuracy of this approximation increases as n increases.
Other extensions include the negative binomial distribution, which deals with the number of trials needed to achieve a fixed number of successes.
Conclusion: Harnessing the Power of Binomial Distributions
The binomial distribution, particularly with parameters like n=20 and p=0.70, is a powerful tool for modeling various real-world phenomena involving a fixed number of independent trials with a constant probability of success. By understanding the formula, calculating probabilities (using software where applicable), and interpreting the mean, variance, and standard deviation, we can gain valuable insights from binomial experiments. Remembering the underlying assumptions and considering potential approximations are crucial for the accurate application of this important statistical model. Mastering the binomial distribution enhances one's ability to analyze data, make informed decisions, and solve problems across a range of disciplines.
Latest Posts
Latest Posts
-
Which Technology Is Shown In The Diagram
Apr 02, 2025
-
Selecciona La Palabra Que No Esta Relacionada
Apr 02, 2025
-
Refer To The Graphic What Type Of Cabling Is Shown
Apr 02, 2025
-
Activity A Continued From Previous Page
Apr 02, 2025
-
Separate But Equal Movie Questions Answer Key
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Consider A Binomial Experiment With N 20 And P 0.70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
