Exhibit 1a-8 Straight Line Relationship Quizlet
Onlines
Apr 01, 2025 · 6 min read
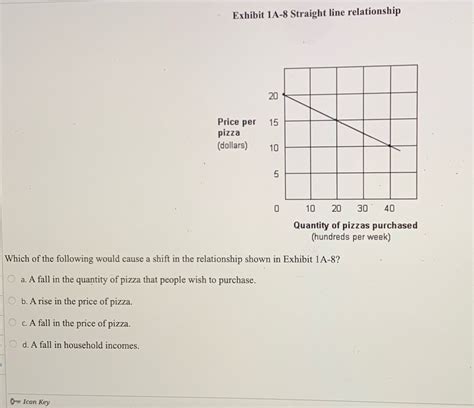
Table of Contents
Decoding Exhibit 1A-8: Mastering the Straight Line Relationship in Data Analysis
Understanding linear relationships is fundamental to various fields, from economics and finance to science and engineering. Exhibit 1A-8, often encountered in data analysis coursework and quizzes (like those found on Quizlet), typically presents a dataset requiring students to identify and interpret a straight-line relationship, or lack thereof. This comprehensive guide will dissect the concept of straight-line relationships, explain how to analyze Exhibit 1A-8-like datasets, and provide strategies for mastering related quiz questions.
What is a Straight-Line Relationship (Linear Relationship)?
A straight-line relationship, or linear relationship, exists between two variables when a change in one variable results in a proportional change in the other. Graphically, this relationship is represented by a straight line. The equation for a straight line is typically expressed as:
y = mx + c
Where:
- y is the dependent variable (the variable whose value depends on another).
- x is the independent variable (the variable that is manipulated or changed).
- m is the slope of the line (representing the rate of change of y with respect to x). A positive slope indicates a positive relationship (as x increases, y increases), while a negative slope indicates a negative relationship (as x increases, y decreases).
- c is the y-intercept (the value of y when x is zero).
Identifying a Straight-Line Relationship in Data:
Analyzing Exhibit 1A-8 (or any similar dataset) to determine if a straight-line relationship exists involves several steps:
1. Data Visualization: The first and often most crucial step is to plot the data points on a scatter plot. This visual representation immediately reveals whether the points tend to cluster around a straight line or not.
2. Calculating the Correlation Coefficient: The correlation coefficient (often denoted as 'r') is a statistical measure that quantifies the strength and direction of a linear relationship between two variables. It ranges from -1 to +1:
- r = +1: Perfect positive linear correlation (a straight line with a positive slope).
- r = -1: Perfect negative linear correlation (a straight line with a negative slope).
- r = 0: No linear correlation (points scattered randomly, no discernible line).
- Values between -1 and +1 indicate varying degrees of linear correlation. The closer 'r' is to +1 or -1, the stronger the linear relationship.
3. Regression Analysis: Regression analysis is a statistical method used to find the best-fitting straight line through the data points. This line, called the regression line, is defined by its slope and y-intercept. The equation of the regression line allows you to predict the value of the dependent variable (y) given a value of the independent variable (x).
Interpreting the Results of the Analysis:
Once you've visualized the data, calculated the correlation coefficient, and potentially performed a regression analysis, you need to interpret the results:
-
Strength of the Relationship: A high absolute value of the correlation coefficient (close to +1 or -1) indicates a strong linear relationship. A low absolute value (close to 0) indicates a weak or no linear relationship.
-
Direction of the Relationship: The sign of the correlation coefficient indicates the direction of the relationship. A positive coefficient indicates a positive relationship (as x increases, y increases), while a negative coefficient indicates a negative relationship (as x increases, y decreases).
-
Significance of the Relationship: Statistical tests (like the t-test) are often used to determine if the observed relationship is statistically significant, meaning it's unlikely to have occurred by chance.
Common Pitfalls to Avoid When Analyzing Exhibit 1A-8-Type Data:
-
Correlation does not equal causation: Just because two variables are strongly correlated doesn't necessarily mean that one causes the other. There might be a third, unobserved variable influencing both.
-
Outliers: Extreme data points (outliers) can significantly influence the correlation coefficient and the regression line. Carefully examine your data for outliers and consider whether they should be included in the analysis. Sometimes, outliers might indicate errors in data collection or other factors that warrant further investigation.
-
Non-linear Relationships: The methods described above are only appropriate for linear relationships. If the data points don't appear to cluster around a straight line, a linear model might not be appropriate. Consider exploring other types of relationships, such as quadratic or exponential relationships.
-
Limited Data: A small sample size can lead to inaccurate conclusions about the relationship between the variables. A larger dataset generally provides a more reliable assessment.
Strategies for Mastering Exhibit 1A-8 Quiz Questions:
-
Practice, Practice, Practice: The key to mastering this topic is consistent practice. Work through numerous examples, focusing on visualizing the data, calculating the correlation coefficient, and interpreting the results.
-
Utilize Visual Aids: Use scatter plots and graphs extensively to visualize the data and identify patterns.
-
Understand the Formulas: Familiarize yourself with the formulas for calculating the correlation coefficient and the equation of a straight line.
-
Develop Intuition: As you work through more examples, you'll develop an intuitive sense of how different data patterns correspond to different correlation coefficients and linear relationships.
-
Seek Clarification: If you're struggling with any aspect of the material, don't hesitate to ask for help from your instructor, classmates, or tutor.
Expanding the Understanding: Beyond the Basics of Exhibit 1A-8
While Exhibit 1A-8 focuses on the fundamental concepts of linear relationships, real-world data analysis often involves more complex scenarios. Here are some advanced aspects to consider:
-
Multiple Regression: This technique extends linear regression to analyze the relationship between a dependent variable and multiple independent variables.
-
Non-linear Regression: When the relationship between variables isn't linear, non-linear regression models, such as polynomial or exponential models, can be employed.
-
Time Series Analysis: This specialized area of statistics deals with data collected over time, often exhibiting trends and seasonality patterns that require specific analytical techniques.
-
Causal Inference: Moving beyond mere correlation, causal inference aims to establish cause-and-effect relationships between variables, often requiring sophisticated statistical methods and experimental designs.
Conclusion:
Mastering the interpretation of straight-line relationships in data, as presented in Exhibit 1A-8 and similar contexts, requires a solid understanding of fundamental statistical concepts and the ability to interpret visual representations of data. By diligently practicing the techniques outlined in this guide, focusing on visualization, and understanding the limitations of linear models, you can confidently tackle any quiz or real-world analysis involving straight-line relationships. Remember, consistent practice and a clear understanding of the underlying principles are the keys to success in this area. The more datasets you analyze and interpret, the more intuitive and efficient your analysis will become. Embrace the challenge, and you will find yourself comfortable and proficient in deciphering the secrets hidden within the seemingly simple straight line.
Latest Posts
Latest Posts
-
Jimena Limpia El Congelador Jimena Esta En
Apr 02, 2025
-
Which Of The Following Is True Of B Cells
Apr 02, 2025
-
Ever 100 Uc Davis Quizlet Final
Apr 02, 2025
-
What Well Known Behaviorist Developed The Hierarchy Of Needs Model
Apr 02, 2025
-
Determine Whether Each Pregnancy Related Statement Is True Or False
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Exhibit 1a-8 Straight Line Relationship Quizlet . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
