Find The Probability That X Falls In The Shaded Area
Onlines
Apr 05, 2025 · 5 min read
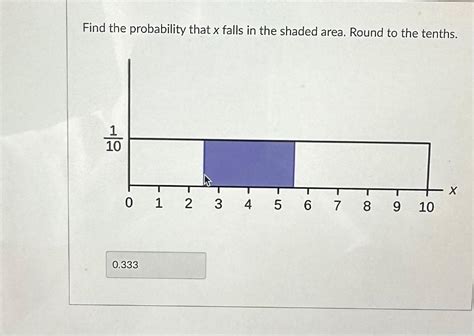
Table of Contents
Find the Probability That X Falls in the Shaded Area: A Comprehensive Guide
Determining the probability that a random variable X falls within a specific shaded area under a probability density function (PDF) is a fundamental concept in statistics and probability theory. This process involves integrating the PDF over the defined region. The complexity of the calculation depends heavily on the shape of the shaded area and the form of the PDF. This article provides a comprehensive guide to tackling this problem, covering various scenarios and techniques.
Understanding Probability Density Functions (PDFs)
Before diving into calculating probabilities, let's review the essential concept of a probability density function. A PDF, denoted as f(x), describes the relative likelihood of a continuous random variable taking on a given value. Crucially, the probability of X falling within a specific interval [a, b] is given by the definite integral of the PDF over that interval:
P(a ≤ X ≤ b) = ∫<sub>a</sub><sup>b</sup> f(x) dx
This integral represents the area under the curve of the PDF between points a and b. The total area under the entire PDF curve always equals 1, reflecting the certainty that X must take on some value.
Common Probability Distributions and their PDFs
Several standard probability distributions are frequently encountered in statistical analysis. Understanding their PDFs is critical for calculating probabilities efficiently. Here are a few examples:
1. Normal Distribution (Gaussian Distribution)
The normal distribution is arguably the most prevalent in statistics. Its PDF is given by:
f(x) = (1 / (σ√(2π))) * e<sup>-((x - μ)<sup>2</sup> / (2σ<sup>2</sup>))</sup>
where:
- μ represents the mean (average) of the distribution.
- σ represents the standard deviation (measure of spread).
The probability of X falling within a specific range requires integrating this complex function, often necessitating numerical methods or using statistical tables (z-tables).
2. Uniform Distribution
The uniform distribution assigns equal probability to all values within a given interval [a, b]. Its PDF is a simple rectangular function:
f(x) = 1 / (b - a) for a ≤ x ≤ b
f(x) = 0 otherwise
Calculating probabilities for a uniform distribution is straightforward, as it involves calculating the area of a rectangle.
3. Exponential Distribution
The exponential distribution is often used to model waiting times or the lifespan of certain systems. Its PDF is:
f(x) = λe<sup>-λx</sup> for x ≥ 0
where λ is the rate parameter. Calculating probabilities involves integrating this function, which results in a relatively simple closed-form solution.
Methods for Calculating Probabilities
The approach to calculating the probability that X falls in the shaded area depends heavily on the shape of the area and the underlying PDF.
1. Direct Integration:
For simpler PDFs and well-defined shaded areas, direct integration offers a precise solution. This involves setting up the appropriate definite integral and solving it analytically. For example, if the shaded area is a simple interval [a, b], the probability is:
P(a ≤ X ≤ b) = ∫<sub>a</sub><sup>b</sup> f(x) dx
However, for complex shapes or intricate PDFs, analytical integration might be intractable.
2. Numerical Integration:
When analytical integration is impractical, numerical methods provide approximations. These methods, such as the trapezoidal rule or Simpson's rule, divide the shaded area into smaller segments and approximate the integral using geometrical techniques. The accuracy of the approximation increases with the number of segments. Software packages like MATLAB, R, or Python (with libraries like SciPy) offer robust numerical integration routines.
3. Monte Carlo Simulation:
Monte Carlo simulation offers a powerful approach, especially for complex scenarios. This involves generating a large number of random samples from the PDF. The proportion of samples falling within the shaded area provides an estimate of the probability. The accuracy of the estimate improves with the number of samples.
4. Using Statistical Tables and Software:
For common distributions like the normal distribution, statistical tables (like z-tables for the standard normal distribution) or statistical software packages (like R, SPSS, or Excel) provide pre-computed probabilities for various intervals. These tools significantly simplify the calculation process.
Examples: Finding Probabilities in Specific Shaded Areas
Let's illustrate the probability calculation with concrete examples:
Example 1: Normal Distribution
Suppose X follows a normal distribution with mean μ = 50 and standard deviation σ = 10. We want to find the probability that X falls within the interval [40, 60]. This involves integrating the normal PDF from 40 to 60. Direct integration is difficult, so we typically use z-tables or software:
-
Standardization: Transform X into a standard normal variable Z using: Z = (X - μ) / σ. This gives Z = (40 - 50) / 10 = -1 and Z = (60 - 50) / 10 = 1.
-
Using Z-table or Software: Look up the probability P(-1 ≤ Z ≤ 1) in a standard normal table or use statistical software. The result is approximately 0.6827. Therefore, P(40 ≤ X ≤ 60) ≈ 0.6827.
Example 2: Uniform Distribution
Let X follow a uniform distribution on the interval [0, 10]. We want to find the probability that X falls within the interval [2, 8].
The PDF is f(x) = 1/10 for 0 ≤ x ≤ 10. The probability is simply the area of the rectangle:
P(2 ≤ X ≤ 8) = (8 - 2) * (1/10) = 0.6
Example 3: Complex Shaded Area
Imagine a shaded area defined by a more complex shape, for instance, the area under a normal curve above a certain threshold or a region between two curves. In such cases, numerical integration or Monte Carlo simulation becomes more practical.
Advanced Considerations and Challenges
Several factors can add complexity to finding probabilities:
-
Multivariate Distributions: When dealing with multiple random variables, the calculation involves multi-dimensional integrals over the shaded region in the multivariate space.
-
Conditional Probabilities: Calculating probabilities conditional on other events further complicates the calculation, often involving conditional PDFs.
-
Bayesian Analysis: In Bayesian contexts, probabilities are updated based on new evidence, requiring iterative calculations using Bayes' theorem.
-
Dealing with Censored or Truncated Data: When dealing with datasets where some values are not fully observed, special techniques are needed to adjust the probability calculations.
Conclusion
Calculating the probability that a random variable falls within a specific shaded area is a cornerstone of statistical analysis. The approach depends strongly on the form of the probability density function and the geometry of the shaded area. While simple cases allow for direct integration, more complex situations may necessitate numerical methods or Monte Carlo simulation. Understanding various probability distributions and selecting the appropriate technique are essential for accurate and efficient probability calculations. Mastering this skill empowers you to effectively analyze data and make informed decisions in various fields.
Latest Posts
Latest Posts
-
What Decision Making Step Is The Mission Statement Developed
Apr 05, 2025
-
A Geographic Combatant Command Is A Category Of Jtf Hq
Apr 05, 2025
-
Drag The Word Parts From The Bank On The Chalkboard
Apr 05, 2025
-
Managerial Strategy Are The Odds In Atlantic Hotels Favor
Apr 05, 2025
-
Their Eyes Were Watching God One Pager
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Find The Probability That X Falls In The Shaded Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
