For Any Integer X X2-x Will Always Produce
Onlines
May 12, 2025 · 5 min read
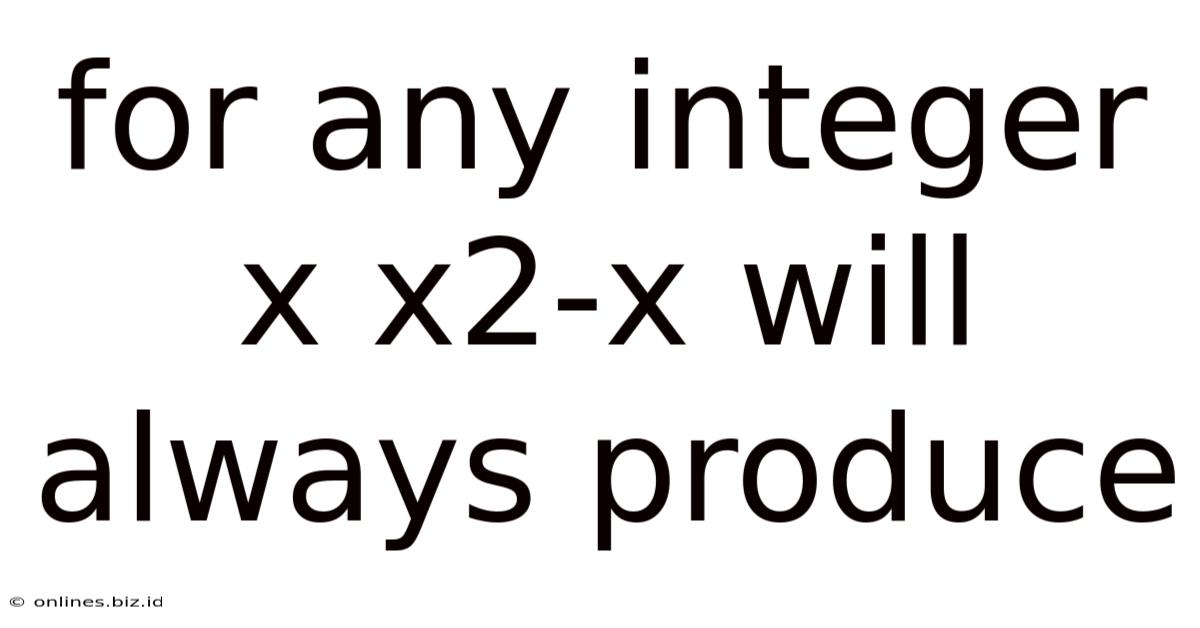
Table of Contents
For Any Integer x, x² - x Will Always Produce an Even Number: A Mathematical Exploration
The statement "for any integer x, x² - x will always produce an even number" is a fascinating mathematical assertion that can be proven through various approaches. This exploration will delve into the intricacies of this statement, providing multiple proofs and examining its broader implications within number theory. We will not only prove the assertion but also explore its relevance in different mathematical contexts, making it accessible to a wider audience.
Understanding the Problem
Before diving into the proofs, let's clarify the core concept. The expression x² - x represents a quadratic function. We're interested in determining the parity (whether it's even or odd) of the result for any integer input 'x'. An even number is any integer divisible by 2, while an odd number leaves a remainder of 1 when divided by 2. Our aim is to demonstrate that for all integer values of x, the result of x² - x will always be an even number.
Proof 1: Factoring and Even Number Properties
This method leverages the fundamental properties of even numbers and the ability to factor the expression.
The Key: An even number can always be expressed as 2 multiplied by an integer (2k, where k is an integer).
-
Factoring the Expression: The expression x² - x can be factored as follows: x² - x = x(x - 1).
-
Analyzing the Factors: Consider two consecutive integers: x and (x - 1). At least one of these integers must be even. Why? Because consecutive integers always alternate between even and odd.
-
Applying the Even Number Property: Since at least one of the factors (x or x - 1) is even, and the other is an integer, their product must be divisible by 2. This directly implies that x(x - 1) = x² - x is an even number.
Proof 2: Using the Parity of Integers
This proof focuses on the even and odd properties of integers and how they interact within the expression.
-
Case 1: x is Even: If x is an even integer, it can be represented as 2k (where k is an integer). Substituting this into our expression: (2k)² - (2k) = 4k² - 2k = 2(2k² - k). Since this is clearly divisible by 2, the result is even.
-
Case 2: x is Odd: If x is an odd integer, it can be represented as 2k + 1 (where k is an integer). Substituting this into our expression: (2k + 1)² - (2k + 1) = (4k² + 4k + 1) - (2k + 1) = 4k² + 2k = 2(2k² + k). Again, this is divisible by 2, proving the result is even.
-
Conclusion: Since the expression yields an even number for both even and odd values of x, we can conclude that x² - x is always even for any integer x.
Proof 3: Mathematical Induction
This rigorous method employs the principle of mathematical induction to prove the assertion for all integers.
-
Base Case: Let's test for x = 1. 1² - 1 = 0, which is an even number. The statement holds true for the base case.
-
Inductive Hypothesis: Assume the statement is true for some arbitrary integer 'n'. That is, n² - n is even.
-
Inductive Step: We need to prove that the statement also holds for n + 1. Let's evaluate (n + 1)² - (n + 1):
(n + 1)² - (n + 1) = n² + 2n + 1 - n - 1 = n² + n = n(n + 1).
Notice that n and (n + 1) are consecutive integers. From our earlier reasoning (Proof 1), the product of two consecutive integers is always even.
-
Conclusion: By the principle of mathematical induction, since the statement holds for the base case and the inductive step, it is true for all integers x.
Visual Representation and Patterns
While mathematical proofs provide rigorous validation, visualizing the pattern can enhance understanding. Consider creating a table of values for x² - x for different integer values of x:
| x | x² - x |
|---|---|
| -3 | 6 |
| -2 | 2 |
| -1 | 0 |
| 0 | 0 |
| 1 | 0 |
| 2 | 2 |
| 3 | 6 |
| 4 | 12 |
| 5 | 20 |
| ... | ... |
Observing the table, the pattern of even numbers becomes readily apparent. This visual confirmation complements the rigorous mathematical proofs.
Applications and Further Exploration
This seemingly simple mathematical property has implications in various areas:
-
Number Theory: This property is fundamental in understanding the divisibility properties of integers and quadratic forms.
-
Computer Science: In algorithms and programming, understanding the parity of numbers can be crucial for optimization and error handling. For instance, it could be used in efficient bit manipulation techniques.
-
Combinatorics: The expression might appear in counting problems or combinatorial identities.
Further exploration could involve investigating similar properties for different polynomial expressions or exploring the behavior of the expression in modular arithmetic. Analyzing the expression modulo various numbers (e.g., modulo 4, modulo 8) could reveal additional patterns and deeper insights into its properties.
Conclusion
The assertion that for any integer x, x² - x will always produce an even number is demonstrably true. We've explored three distinct proofs – factoring, parity analysis, and mathematical induction – each providing a different perspective on this fundamental property. Beyond the rigorous mathematical proofs, visualizing the pattern and understanding its potential applications in other mathematical fields enrich our comprehension. This simple yet powerful result highlights the elegance and interconnectedness of mathematical concepts, underscoring the beauty of number theory. The exploration of this seemingly basic property provides a solid foundation for venturing into more complex mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
The Dirty Harry Problem Refers To
May 12, 2025
-
What European Industries Benefited From African Resources
May 12, 2025
-
What Is The Relationship Between Co2 And O2 For Kelp
May 12, 2025
-
What Is Revealed About Jay Gatsby Aka James Gatz
May 12, 2025
-
Establishing A Team Identity Is Facilitated By
May 12, 2025
Related Post
Thank you for visiting our website which covers about For Any Integer X X2-x Will Always Produce . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.