Identifying Transformations Worksheet Homework 5 Answer Key
Onlines
Mar 30, 2025 · 6 min read
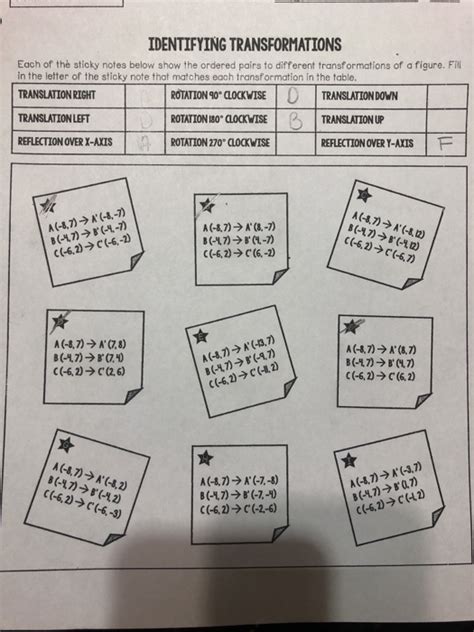
Table of Contents
Identifying Transformations: A Comprehensive Guide with Worksheet Solutions
Identifying geometric transformations is a crucial skill in mathematics, particularly in geometry and algebra. Understanding translations, rotations, reflections, and dilations is fundamental for higher-level mathematical concepts. This comprehensive guide will delve into each transformation type, providing clear explanations, illustrative examples, and, most importantly, detailed solutions to a sample "Identifying Transformations Worksheet Homework 5." We'll also explore strategies to effectively approach these types of problems and enhance your problem-solving skills.
Understanding the Four Main Transformations
Before diving into the worksheet, let's solidify our understanding of the four primary geometric transformations:
1. Translation
A translation is a transformation that moves every point of a figure the same distance in the same direction. Think of it as sliding the figure without rotating or changing its size or shape. Translations are described using vector notation, often represented as <x, y>, where 'x' indicates the horizontal shift and 'y' the vertical shift. A positive x value means a shift to the right, a negative x value to the left. Similarly, a positive y value signifies an upward shift, and a negative y value a downward shift.
2. Rotation
A rotation involves turning a figure around a fixed point called the center of rotation. The rotation is defined by the angle of rotation (how many degrees the figure is turned) and the direction of rotation (clockwise or counterclockwise). A positive angle typically indicates a counterclockwise rotation, and a negative angle a clockwise rotation. The center of rotation can be within the figure, outside the figure, or even on the figure itself.
3. Reflection
A reflection is a transformation that flips a figure across a line called the line of reflection (or axis of reflection). Each point in the reflected figure is the same distance from the line of reflection as its corresponding point in the original figure. The line of reflection acts like a mirror, producing a mirror image of the original figure.
4. Dilation
A dilation changes the size of a figure. It's a transformation that stretches or shrinks a figure while maintaining its shape. A dilation is defined by a scale factor, which determines the size change. A scale factor greater than 1 enlarges the figure, while a scale factor between 0 and 1 shrinks the figure. A scale factor of 1 results in no change (the figure remains the same size). The dilation is performed with respect to a center of dilation, which can be inside, outside, or on the figure.
Sample "Identifying Transformations Worksheet Homework 5" Problems and Solutions
Let's now tackle a hypothetical "Identifying Transformations Worksheet Homework 5." We'll work through several problems, illustrating the concepts and providing detailed explanations.
Problem 1:
The point A(2, 3) is translated to A'(5, 1). Describe the translation using vector notation.
Solution:
The x-coordinate changes from 2 to 5 (an increase of 3), and the y-coordinate changes from 3 to 1 (a decrease of 2). Therefore, the translation vector is <3, -2>.
Problem 2:
Triangle ABC with vertices A(1, 1), B(3, 1), and C(2, 3) is reflected across the x-axis. Find the coordinates of the vertices of the reflected triangle A'B'C'.
Solution:
Reflection across the x-axis changes the sign of the y-coordinate while keeping the x-coordinate the same. Therefore:
- A(1, 1) becomes A'(1, -1)
- B(3, 1) becomes B'(3, -1)
- C(2, 3) becomes C'(2, -3)
Problem 3:
Quadrilateral ABCD is rotated 90 degrees counterclockwise about the origin. If A=(1,2), B=(3,2), C=(3,4), and D=(1,4), find the coordinates of A'B'C'D'.
Solution:
A 90-degree counterclockwise rotation about the origin transforms a point (x, y) to (-y, x). Therefore:
- A(1, 2) becomes A'(-2, 1)
- B(3, 2) becomes B'(-2, 3)
- C(3, 4) becomes C'(-4, 3)
- D(1, 4) becomes D'(-4, 1)
Problem 4:
Triangle DEF with vertices D(2, 2), E(4, 2), and F(3, 4) is dilated with a scale factor of 2 and a center of dilation at the origin (0,0). Find the coordinates of the vertices of the dilated triangle D'E'F'.
Solution:
A dilation with a scale factor of 2 centered at the origin multiplies both coordinates of each point by 2. Therefore:
- D(2, 2) becomes D'(4, 4)
- E(4, 2) becomes E'(8, 4)
- F(3, 4) becomes F'(6, 8)
Problem 5:
Identify the transformation that maps triangle PQR onto triangle P'Q'R'. The coordinates are P(1, 2), Q(3, 2), R(2, 4) and P'(-1, 2), Q'(-3, 2), R'(-2, 4).
Solution:
Observe that the y-coordinates remain unchanged, while the x-coordinates have changed sign. This indicates a reflection across the y-axis.
Problem 6 (More Challenging):
A figure is transformed through a sequence of transformations: first, a translation of <2, -1>, then a reflection across the x-axis, and finally, a dilation with a scale factor of 1/2 centered at the origin. If the final image of a point is (1, -1), find the original coordinates of the point.
Solution: This problem requires working backward through the transformations:
-
Undo the dilation: Since the dilation had a scale factor of 1/2, we multiply the final coordinates by 2: (2, -2).
-
Undo the reflection: A reflection across the x-axis changes the sign of the y-coordinate. Therefore, the coordinates become (2, 2).
-
Undo the translation: The translation was
<2, -1>. To undo it, we subtract 2 from the x-coordinate and add 1 to the y-coordinate: (0, 3).
Therefore, the original coordinates of the point were (0, 3).
Strategies for Success in Identifying Transformations
Mastering the identification of geometric transformations involves a systematic approach:
-
Visual Inspection: Carefully examine the original and transformed figures. Look for patterns in the movement, size changes, or orientation shifts.
-
Coordinate Analysis: Compare the coordinates of corresponding points in the original and transformed figures. Look for consistent changes in the x and y values, which will help identify the type and specifics of the transformation.
-
Rule Application: Memorize the rules for each transformation type (e.g., reflection across the x-axis changes the sign of the y-coordinate). Apply these rules systematically to verify your observations.
-
Step-by-Step Approach: For complex transformations involving multiple steps, work through each step individually, starting with the last transformation and working backward.
-
Practice, Practice, Practice: The more you practice solving problems involving geometric transformations, the more comfortable and proficient you will become.
Conclusion
Identifying geometric transformations is a fundamental skill in mathematics. By understanding the four main types of transformations – translation, rotation, reflection, and dilation – and by applying a systematic approach to problem-solving, you can successfully tackle even complex transformation problems. This guide, complete with solved examples, provides a solid foundation for mastering this crucial mathematical concept. Remember to practice regularly to solidify your understanding and build confidence in your problem-solving abilities. With consistent effort, you’ll soon be able to identify any transformation with ease.
Latest Posts
Latest Posts
-
Quentin A Lead Dentist Is Supervising A Dental Trainee
Apr 01, 2025
-
Chapter 1 Summary Of The Hobbit
Apr 01, 2025
-
Sociologists Use The Term Empirical Evidence To Refer To
Apr 01, 2025
-
How Can Presenters Best Address Two Sides Of An Issue
Apr 01, 2025
-
Successful Teams Share Several Characteristics For Example Successful Teams
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Identifying Transformations Worksheet Homework 5 Answer Key . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
