Intermediate Math Concepts 6.2 Special Right Triangles
Onlines
Mar 30, 2025 · 6 min read
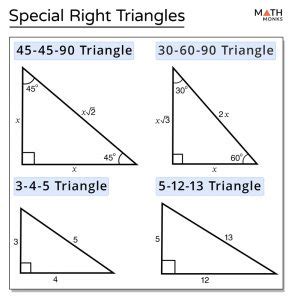
Table of Contents
- Intermediate Math Concepts 6.2 Special Right Triangles
- Table of Contents
- Intermediate Math Concepts: 6.2 Special Right Triangles
- Understanding the Fundamentals: What are Special Right Triangles?
- Key Characteristics:
- Type 1: The 45-45-90 Triangle (Isosceles Right Triangle)
- Side Ratio:
- Example Problems:
- Type 2: The 30-60-90 Triangle
- Side Ratio:
- Example Problems:
- Practical Applications and Real-World Examples
- Advanced Applications and Extensions
- Common Mistakes to Avoid
- Tips for Mastering Special Right Triangles
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Intermediate Math Concepts: 6.2 Special Right Triangles
Understanding special right triangles is a crucial stepping stone in your mathematical journey. These triangles, with their specific angle measurements and side ratios, provide shortcuts and efficiency in solving various geometric problems. This in-depth guide will explore the two primary types – 45-45-90 triangles and 30-60-90 triangles – providing you with a solid foundation in their properties and applications.
Understanding the Fundamentals: What are Special Right Triangles?
Special right triangles are right-angled triangles (containing one 90° angle) with specific angle measures that lead to predictable ratios between their side lengths. This predictability eliminates the need for complex trigonometric functions in many cases, offering quicker and simpler solutions. These consistent ratios are invaluable tools in geometry, trigonometry, and even calculus.
Mastering these triangles will significantly improve your problem-solving skills, saving you time and effort in various mathematical contexts.
Key Characteristics:
- Right Angle: All special right triangles contain a 90° angle.
- Specific Angle Measures: The remaining two angles are always specific values (45°, 45° for one type and 30°, 60° for the other).
- Consistent Side Ratios: The lengths of the sides follow consistent ratios, irrespective of the triangle's size. This is the most crucial feature, allowing for rapid calculations.
Type 1: The 45-45-90 Triangle (Isosceles Right Triangle)
The 45-45-90 triangle, also known as an isosceles right triangle, is characterized by two equal angles (45°) and one right angle (90°). Because two angles are equal, this means that the two legs (the sides adjacent to the right angle) are also equal in length.
Side Ratio:
The side ratio of a 45-45-90 triangle is always 1:1:√2. This means:
- Leg 1 = Leg 2 = x (where 'x' is a variable representing the length)
- Hypotenuse = x√2 (the hypotenuse is the side opposite the right angle)
This simple ratio makes calculations straightforward. If you know the length of one leg, you can easily determine the lengths of the other two sides.
Example Problems:
Problem 1: A 45-45-90 triangle has a leg of length 5 cm. Find the length of the hypotenuse.
Solution: Since the leg length is 5 cm, we know x = 5. Therefore, the hypotenuse is x√2 = 5√2 cm.
Problem 2: The hypotenuse of a 45-45-90 triangle measures 10√2 inches. Find the length of each leg.
Solution: We have x√2 = 10√2. Dividing both sides by √2 gives x = 10 inches. Therefore, each leg measures 10 inches.
Type 2: The 30-60-90 Triangle
The 30-60-90 triangle is another special right triangle, distinguished by its angles: a 30° angle, a 60° angle, and a right angle (90°). This triangle's side lengths are related in a specific ratio.
Side Ratio:
The side ratio for a 30-60-90 triangle is 1:√3:2. This means:
- Shortest Side (opposite the 30° angle) = x
- Longer Leg (opposite the 60° angle) = x√3
- Hypotenuse = 2x
Understanding this ratio is key to quickly solving problems involving 30-60-90 triangles.
Example Problems:
Problem 1: A 30-60-90 triangle has a hypotenuse of length 12 meters. Find the lengths of the other two sides.
Solution: We know 2x = 12 meters, so x = 6 meters (the shortest side). The longer leg is x√3 = 6√3 meters.
Problem 2: The shorter leg of a 30-60-90 triangle measures 4 inches. Find the length of the hypotenuse and the longer leg.
Solution: Since the shorter leg is 4 inches, x = 4 inches. The hypotenuse is 2x = 8 inches. The longer leg is x√3 = 4√3 inches.
Practical Applications and Real-World Examples
The applications of special right triangles extend beyond theoretical mathematics, finding practical use in various fields:
-
Engineering and Architecture: Calculating distances, heights, and angles in construction projects, structural design, and surveying. Imagine determining the height of a building using the angle of elevation and the distance from the building. A 30-60-90 triangle can simplify this calculation.
-
Physics: Analyzing projectile motion, calculating vectors, and solving problems related to forces and motion. Many physics problems use right triangles to break down forces into their components.
-
Computer Graphics and Game Development: Creating realistic 3D models and animations relies heavily on geometrical calculations, including special right triangles, to accurately represent angles and distances.
-
Navigation: Determining distances and bearings using triangulation techniques. Special right triangles can help simplify calculations in navigation problems.
-
Cartography (Mapmaking): Calculating distances and areas on maps often involves using special right triangles.
Advanced Applications and Extensions
While the basic applications involve simple calculations of side lengths, the principles of special right triangles extend to more complex scenarios:
-
Trigonometry: Special right triangles provide a concrete foundation for understanding trigonometric ratios (sine, cosine, tangent) before progressing to more advanced trigonometric identities and equations.
-
Calculus: Understanding the relationships between side lengths in special right triangles is essential when dealing with geometrical problems in calculus, such as finding areas and volumes.
-
Coordinate Geometry: Special right triangles help in understanding distances and slopes within coordinate systems, simplifying the process of determining the distance between two points or finding the equation of a line.
Common Mistakes to Avoid
-
Confusing the Ratios: Make sure you thoroughly understand and memorize the correct side ratios for both 45-45-90 and 30-60-90 triangles. Mixing them up will lead to incorrect calculations.
-
Incorrectly Applying the Ratios: Always identify which side is 'x' (the shortest side in a 30-60-90 triangle or a leg in a 45-45-90 triangle) before applying the ratio. Misidentifying 'x' will result in errors.
-
Approximating √2 and √3: While approximations are sometimes necessary, try to keep your answers in radical form (e.g., 5√2) as long as possible to maintain accuracy. Only approximate at the final step if needed.
-
Overlooking the Right Angle: Always remember that these are right-angled triangles. The right angle is crucial in applying the special triangle rules.
Tips for Mastering Special Right Triangles
-
Practice Regularly: Solve numerous problems of varying complexity to build your intuition and confidence. The more problems you solve, the better you’ll understand the concepts.
-
Visualize: Draw diagrams of the triangles to help you visualize the relationships between the angles and sides.
-
Use Flashcards: Create flashcards to memorize the angle measures and side ratios to aid quick recall during problem-solving.
-
Seek Help When Needed: Don't hesitate to ask for clarification from your teacher, tutor, or peers if you encounter difficulties. Understanding these concepts is essential for future mathematical success.
Conclusion
Special right triangles, despite their seemingly simple nature, represent a fundamental concept with widespread applications across various mathematical fields and real-world scenarios. By mastering their properties and applying the correct ratios, you'll significantly enhance your problem-solving capabilities and gain a deeper appreciation for the elegance and power of geometry. Consistent practice and a clear understanding of the fundamental concepts will pave your way to successfully tackling more advanced mathematical challenges. Remember, the key is to understand the underlying relationships between the angles and sides, and to practice applying those relationships in a variety of problem-solving scenarios. With enough effort, mastering special right triangles will become second nature, and you'll reap the benefits in your mathematical journey.
Latest Posts
Latest Posts
-
Enemies From Within Speech Answer Key
Apr 03, 2025
-
Chapter 11 Their Eyes Were Watching God
Apr 03, 2025
-
Chapter 15 Nutrition And Hydration Workbook Answers
Apr 03, 2025
-
The God Of Small Things Chapter 1 Summary
Apr 03, 2025
-
Speak By Laurie Halse Anderson Summary
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Intermediate Math Concepts 6.2 Special Right Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
