Lesson 3 Comprehending And Analyzing Series Rlc Circuits
Onlines
Apr 05, 2025 · 7 min read
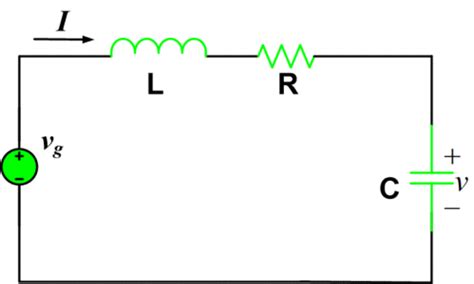
Table of Contents
Lesson 3: Comprehending and Analyzing Series RLC Circuits
This lesson delves into the intricacies of series RLC circuits, providing a comprehensive understanding of their behavior and analysis techniques. We'll move beyond basic concepts to explore resonant frequency, bandwidth, quality factor (Q factor), and transient responses, equipping you with the knowledge to design and troubleshoot these crucial circuits.
Understanding the Series RLC Circuit
A series RLC circuit consists of a resistor (R), an inductor (L), and a capacitor (C) connected in series. This seemingly simple configuration exhibits surprisingly complex behavior, particularly when driven by an AC source. The interaction between the components leads to phenomena like resonance, which has significant implications in various applications.
Component Interactions
-
Resistor (R): The resistor dissipates energy in the form of heat, affecting the overall circuit efficiency and damping the oscillations. It contributes to the overall impedance of the circuit.
-
Inductor (L): The inductor stores energy in a magnetic field. Its impedance, called inductive reactance (XL), is directly proportional to the frequency of the applied signal (XL = 2πfL, where f is the frequency and L is the inductance).
-
Capacitor (C): The capacitor stores energy in an electric field. Its impedance, called capacitive reactance (XC), is inversely proportional to the frequency (XC = 1/(2πfC), where f is the frequency and C is the capacitance).
The interplay between the inductive and capacitive reactances is the key to understanding the resonant behavior of the series RLC circuit.
Resonance in Series RLC Circuits
Resonance occurs when the inductive reactance (XL) and capacitive reactance (XC) cancel each other out. This means the impedance of the circuit is at its minimum, allowing maximum current to flow for a specific frequency. This frequency is known as the resonant frequency (fr).
Calculating Resonant Frequency
The resonant frequency (fr) can be calculated using the following formula:
fr = 1 / (2π√(LC))
At resonance:
- XL = XC
- Impedance (Z) is minimal and equal to R.
- Current (I) is maximal.
- Voltage across the inductor (VL) and capacitor (VC) are equal in magnitude but 180 degrees out of phase.
The resonant frequency is a crucial parameter in designing filters and oscillators. By carefully selecting the inductance (L) and capacitance (C), the circuit can be tuned to resonate at a specific frequency, selectively amplifying or attenuating signals at that frequency.
Impact of Resistance
The resistor (R) in the series RLC circuit doesn't directly affect the resonant frequency, but it significantly influences the circuit's behavior around the resonant frequency. A higher resistance leads to a broader resonance curve (lower Q factor), meaning the circuit is less selective in its frequency response. A lower resistance leads to a sharper resonance curve (higher Q factor), resulting in a more selective response.
Quality Factor (Q Factor)
The quality factor (Q factor) is a dimensionless parameter that describes the sharpness of the resonance curve. It represents the ratio of energy stored in the reactive components (L and C) to the energy dissipated in the resistor (R) per cycle. A higher Q factor indicates a sharper resonance, while a lower Q factor implies a broader resonance.
Calculating Q Factor
The Q factor for a series RLC circuit is calculated as:
Q = (1/R)√(L/C)
A high Q factor signifies a highly selective circuit, capable of filtering out unwanted frequencies effectively. Conversely, a low Q factor implies a less selective circuit. The Q factor is directly related to the bandwidth of the circuit, which we will discuss next.
Bandwidth
Bandwidth is the range of frequencies over which the circuit's output power remains above a certain level (typically 70.7% of the maximum power at resonance, also known as the half-power points). This is directly related to the Q factor.
Calculating Bandwidth
The bandwidth (BW) of a series RLC circuit can be calculated using the following formula:
BW = fr / Q
A higher Q factor leads to a narrower bandwidth, meaning the circuit is more selective. Conversely, a lower Q factor results in a wider bandwidth, meaning the circuit is less selective. The choice of bandwidth is crucial in filter design, determining the circuit's ability to pass or reject specific frequency ranges.
Transient Response
The transient response of a series RLC circuit describes its behavior when subjected to a sudden change in voltage or current, such as switching the circuit on or off. The response depends on the relationship between R, L, and C, leading to three distinct types of responses:
-
Underdamped: The circuit oscillates before settling to a steady state. This occurs when the resistance is relatively low compared to the inductance and capacitance. The oscillations decay gradually over time.
-
Critically Damped: The circuit reaches the steady state as quickly as possible without oscillating. This represents the optimal damping condition, achieving a fast response without overshoot.
-
Overdamped: The circuit slowly approaches the steady state without oscillating. This happens when the resistance is relatively high compared to the inductance and capacitance. The response is slow but avoids oscillations.
The transient response is crucial in applications where fast and stable responses are essential, like switching power supplies and control systems.
Applications of Series RLC Circuits
Series RLC circuits find widespread applications in various electronic systems, including:
-
Filters: Series RLC circuits form the basis of various filter types, such as bandpass filters (allowing a specific range of frequencies to pass) and band-stop filters (blocking a specific range of frequencies). These filters are vital in signal processing and communication systems.
-
Resonant Circuits: They are used in resonant circuits for tuning radio receivers, selecting specific frequencies from a broad spectrum of signals. This is crucial in radio and television broadcasting.
-
Oscillators: Series RLC circuits can be integrated into oscillator circuits to generate sinusoidal waveforms at the resonant frequency. These circuits are crucial in signal generation and timing applications.
-
Power Supplies: They play a role in power supplies, particularly in smoothing the output voltage and reducing ripple.
-
Impedance Matching: In some applications, they are utilized for impedance matching, optimizing power transfer between different components of a system.
Analyzing Series RLC Circuits: Methods and Tools
Analyzing series RLC circuits often involves determining the circuit's impedance, current, voltage across each component, and the phase relationships between them. Several methods can be used:
-
Ohm's Law and Impedance Calculations: Using Ohm's law (V = IZ) and calculating the impedance (Z) of the circuit, which involves considering the resistance (R), inductive reactance (XL), and capacitive reactance (XC). The total impedance is given by Z = √(R² + (XL - XC)²).
-
Kirchhoff's Laws: Applying Kirchhoff's voltage law (KVL) helps solve for voltages and currents in the circuit.
-
Phasor Diagrams: These diagrams help visualize the phase relationships between voltages and currents in the circuit, providing a clear representation of the circuit's behavior.
-
Circuit Simulation Software: Tools like LTSpice, Multisim, and others offer powerful simulation capabilities, allowing designers to analyze circuit behavior before physical implementation. They are particularly useful for complex circuits or for investigating transient responses.
Troubleshooting Series RLC Circuits
Troubleshooting involves systematically identifying and resolving issues in the circuit. Some common problems include:
-
Open Circuits: An open circuit in any component will prevent current flow, leading to a malfunction.
-
Short Circuits: A short circuit can cause excessive current flow, potentially damaging components.
-
Component Failures: Failed capacitors, inductors, or resistors can cause unexpected circuit behavior.
-
Incorrect Component Values: Using incorrect component values will deviate the circuit's operation from the designed parameters.
Systematic testing with a multimeter, checking component values, and utilizing circuit analysis techniques are crucial in diagnosing and rectifying such problems.
Conclusion
Series RLC circuits, while seemingly simple, exhibit rich and complex behaviors. Understanding concepts like resonant frequency, Q factor, bandwidth, and transient response is critical for designing and analyzing various electronic circuits. Mastering the techniques presented in this lesson will enable you to tackle advanced circuit analysis and design problems effectively. The applications of these circuits are vast, spanning across diverse fields in electronics and communication engineering. Remember to utilize simulation tools and systematic troubleshooting techniques to ensure successful design and operation.
Latest Posts
Latest Posts
-
Advancement Selection Board Panel Members Review
Apr 05, 2025
-
Bbc Battle Of The Brains Worksheet Answers
Apr 05, 2025
-
The Primary Concerns When First Starting Your Business Are
Apr 05, 2025
-
Access Privilege To Protected Health Information Is
Apr 05, 2025
-
Your Life Your Money Worksheet Answers
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Lesson 3 Comprehending And Analyzing Series Rlc Circuits . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
