Quiz 4-1 Classifying And Solving For Sides
Onlines
Apr 03, 2025 · 7 min read
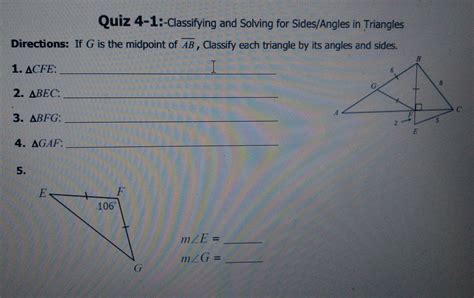
Table of Contents
Quiz 4-1: Classifying and Solving for Sides of Triangles
This comprehensive guide delves into the intricacies of classifying triangles based on their sides and angles, and then focuses on solving for unknown side lengths using various techniques. We'll cover fundamental concepts, practical examples, and problem-solving strategies to solidify your understanding. This is ideal for students preparing for a quiz on this topic or anyone seeking a deeper comprehension of triangle geometry.
Understanding Triangle Classification
Before tackling side-length calculations, it's crucial to understand how triangles are classified. Triangles are categorized based on two key characteristics: their side lengths and their angles.
Classification by Side Lengths:
-
Equilateral Triangles: These triangles possess three sides of equal length. This equality results in three equal angles, each measuring 60 degrees. Think of an equilateral triangle as a perfectly symmetrical shape.
-
Isosceles Triangles: Isosceles triangles have at least two sides of equal length. These equal sides are often called "legs," while the third side is called the "base." The angles opposite the equal sides are also equal.
-
Scalene Triangles: Scalene triangles are characterized by having all three sides of different lengths. Consequently, all three angles will also have different measures.
Classification by Angles:
-
Acute Triangles: All three angles in an acute triangle are less than 90 degrees.
-
Right Triangles: Right triangles contain one 90-degree angle (a right angle). The side opposite the right angle is called the hypotenuse, and the other two sides are called legs.
-
Obtuse Triangles: Obtuse triangles have one angle greater than 90 degrees.
Important Note: A triangle can be classified in multiple ways. For example, a triangle can be both an isosceles triangle and an acute triangle.
Solving for Unknown Side Lengths
Now let's move on to the core of this topic: determining the lengths of unknown sides within a triangle. The methods used depend heavily on the type of triangle and the information provided.
1. Using the Pythagorean Theorem (Right Triangles Only)
The Pythagorean Theorem is a cornerstone of right-triangle geometry. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs).
Formula: a² + b² = c²
Where:
- 'a' and 'b' are the lengths of the legs.
- 'c' is the length of the hypotenuse.
Example:
A right-angled triangle has legs of length 3 cm and 4 cm. Find the length of the hypotenuse.
Solution:
- Substitute the values into the Pythagorean Theorem: 3² + 4² = c²
- Simplify: 9 + 16 = c²
- Solve for c: c² = 25 => c = 5 cm
This theorem is fundamental and should be thoroughly understood. Practice solving various problems to master its application.
2. Using Trigonometry (Right Triangles)
Trigonometric functions (sine, cosine, and tangent) provide powerful tools for solving right-angled triangles when you know one angle and one side length.
Definitions:
- sin θ = opposite / hypotenuse
- cos θ = adjacent / hypotenuse
- tan θ = opposite / adjacent
Where:
- θ is the angle in question.
- "opposite" refers to the side opposite the angle.
- "adjacent" refers to the side next to the angle (not the hypotenuse).
- "hypotenuse" is the side opposite the right angle.
Example:
In a right-angled triangle, one angle is 30 degrees, and the hypotenuse is 10 cm. Find the length of the side opposite the 30-degree angle.
Solution:
- Use the sine function: sin 30° = opposite / 10 cm
- Solve for the opposite side: opposite = 10 cm * sin 30° => opposite = 5 cm
3. Using the Law of Sines (Any Triangle)
The Law of Sines is applicable to any triangle, not just right-angled ones. It establishes a relationship between the angles and the lengths of the sides opposite them.
Formula: a/sin A = b/sin B = c/sin C
Where:
- a, b, and c are the lengths of the sides.
- A, B, and C are the angles opposite those sides.
Example:
A triangle has angles A = 40°, B = 60°, and side a = 8 cm. Find the length of side b.
Solution:
- Use the Law of Sines: 8 cm / sin 40° = b / sin 60°
- Solve for b: b = (8 cm * sin 60°) / sin 40° (You'll need a calculator to find the sine values and solve for b).
4. Using the Law of Cosines (Any Triangle)
The Law of Cosines is another powerful tool for solving any triangle, particularly useful when you know two sides and the included angle or all three sides.
Formulas:
- a² = b² + c² - 2bc cos A
- b² = a² + c² - 2ac cos B
- c² = a² + b² - 2ab cos C
Where:
- a, b, and c are the lengths of the sides.
- A, B, and C are the angles opposite those sides.
Example:
A triangle has sides a = 5 cm, b = 7 cm, and angle C = 60°. Find the length of side c.
Solution:
- Use the Law of Cosines: c² = 5² + 7² - 2 * 5 * 7 * cos 60°
- Simplify and solve for c: c² = 25 + 49 - 70 * (1/2) => c² = 34 => c = √34 cm
Solving Triangles: A Step-by-Step Approach
To effectively solve for unknown sides in a triangle, follow this structured approach:
-
Identify the Type of Triangle: Is it a right-angled triangle, an isosceles triangle, a scalene triangle, or a combination? This determines the applicable methods.
-
Identify the Known Information: What side lengths and angles are already known?
-
Choose the Appropriate Method: Select the most suitable formula or technique based on the known information. For right-angled triangles, the Pythagorean Theorem and trigonometric functions are usually the best choices. For other triangles, the Law of Sines or the Law of Cosines may be necessary.
-
Apply the Formula: Substitute the known values into the chosen formula.
-
Solve for the Unknown: Perform the calculations to find the length of the unknown side. Ensure you use a calculator for trigonometric functions and square roots.
-
Check your Answer: Verify your answer to ensure it makes sense in the context of the problem. Consider the relative sizes of the sides and angles. For example, the longest side should be opposite the largest angle.
Advanced Applications and Problem Solving
The principles discussed above are foundational, but mastering triangle geometry involves applying them in diverse scenarios. Here are some advanced applications:
-
Area Calculations: Once side lengths are known, you can calculate the area of a triangle using various formulas, including Heron's formula (for any triangle) or the formula (1/2) * base * height (for right-angled triangles).
-
Coordinate Geometry: Solving triangles can be integrated with coordinate geometry problems, involving finding distances between points and determining the coordinates of vertices.
-
Vectors: Vector methods can be employed to solve for side lengths and angles in triangles, particularly when dealing with directed line segments.
-
Three-Dimensional Geometry: Triangle geometry extends to three-dimensional shapes and their properties.
Practice Problems
To solidify your understanding, work through these practice problems:
-
A right-angled triangle has legs of length 6 cm and 8 cm. Find the length of the hypotenuse.
-
A right-angled triangle has a hypotenuse of length 12 cm and one angle of 35 degrees. Find the lengths of the two legs.
-
A triangle has sides of length 5 cm, 7 cm, and an angle of 70 degrees between them. Find the length of the third side.
-
A triangle has angles A = 50°, B = 70°, and side a = 10 cm. Find the lengths of sides b and c.
Conclusion
Mastering the classification and side-length calculation of triangles is a cornerstone of geometry. By understanding the different types of triangles, applying the Pythagorean theorem, trigonometric functions, and the Laws of Sines and Cosines, you can effectively solve a wide range of problems. Remember to systematically approach each problem, choosing the appropriate method, and always checking your answer for reasonableness. With consistent practice and a firm grasp of the underlying principles, you’ll become proficient in solving any triangle-related challenge. Continue practicing, explore more advanced applications, and enjoy the rewarding journey of mastering this fundamental area of mathematics.
Latest Posts
Latest Posts
-
Guanzon V State Medical Board Of Ohio
Apr 04, 2025
-
Comparing Presidents Foreign And Domestic Policies
Apr 04, 2025
-
Which Is The Best Strategic Therapeutic Consideration For Older Adults
Apr 04, 2025
-
Accounting Information Is Considered To Be Relevant When It
Apr 04, 2025
-
Answers To Cpr Test American Red Cross
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Quiz 4-1 Classifying And Solving For Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
