Spatial Vis Slopes And Curves Answers
Onlines
Mar 29, 2025 · 6 min read
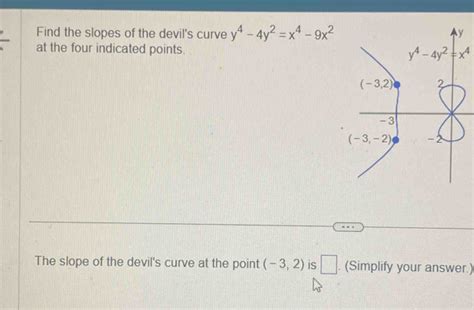
Table of Contents
Spatial Visualization: Mastering Slopes and Curves
Spatial visualization, the ability to mentally manipulate objects in three-dimensional space, is a crucial skill across numerous fields. From architecture and engineering to medicine and gaming, understanding and interpreting slopes and curves is paramount. This comprehensive guide delves into the intricacies of spatial visualization, focusing specifically on slopes and curves, providing you with practical techniques and exercises to hone your skills.
Understanding Slopes: More Than Just a Line
A slope, in its simplest form, represents the steepness or incline of a line. While seemingly basic, grasping the concept of slope extends far beyond simple linear representations. It forms the foundation for understanding gradients, gradients of curves, and even more complex three-dimensional structures.
Defining Slope: Rise Over Run
The fundamental formula for calculating slope is rise over run. Rise refers to the vertical change, while run signifies the horizontal change between two points on a line. A positive slope indicates an upward incline from left to right, while a negative slope indicates a downward incline. A slope of zero represents a horizontal line, and an undefined slope corresponds to a vertical line.
Example: Consider two points: (2, 1) and (4, 5). The rise is 5 - 1 = 4, and the run is 4 - 2 = 2. Therefore, the slope is 4/2 = 2.
Visualizing Slopes in Different Contexts
Beyond simple lines, slopes manifest in various contexts:
-
Topographic Maps: Contour lines on maps represent lines of equal elevation. The closer the contour lines, the steeper the slope. Imagine hiking – closely packed contour lines signify a challenging climb.
-
Three-Dimensional Objects: Consider a ramp or a roof. The slope determines the angle of ascent or descent. Understanding slopes helps in calculating the materials needed and ensuring structural integrity.
-
Data Visualization: Graphs and charts utilize slopes to represent trends and changes over time. A steep positive slope indicates rapid growth, while a shallow slope suggests gradual change.
-
Engineering Design: Slopes are critical in civil engineering, road construction, and even designing drainage systems. Appropriate slopes are essential for safety and functionality.
Advanced Slope Concepts: Gradients and Tangents
-
Gradients: In calculus, the gradient represents the instantaneous rate of change of a function at a specific point. For curves, the gradient at a point is the slope of the tangent line at that point.
-
Tangents: A tangent line touches a curve at a single point without intersecting it (except in special cases). The slope of the tangent line represents the instantaneous rate of change of the curve at that point. Visualizing tangents is essential in understanding the behavior of functions.
Mastering Curves: Beyond Linearity
Curves represent a departure from linearity, introducing complexity and dynamism to spatial visualization. Understanding curves necessitates grappling with their various properties and representations.
Types of Curves: A Diverse Landscape
Numerous types of curves exist, each with unique characteristics:
-
Parabolas: Defined by a quadratic equation, parabolas are U-shaped curves. They represent trajectories of projectiles under gravity and have applications in optics and antenna design.
-
Circles: Defined by a constant distance from a central point, circles are fundamental geometric shapes. Understanding their properties, such as radius and circumference, is critical.
-
Ellipses: Similar to circles but with two focal points, ellipses exhibit varying curvature. Planetary orbits are often elliptical.
-
Hyperbolas: Defined by the difference in distances to two focal points, hyperbolas have two separate branches. They appear in various physics phenomena, including the paths of certain comets.
-
Spirals: Curves that continuously turn around a central point, spirals are seen in nature (e.g., seashells) and engineering (e.g., helical staircases).
-
Cubic and Higher-Order Curves: These are defined by polynomial equations of degree three or higher and exhibit more complex shapes. They are often used in computer-aided design (CAD) and modeling.
Visualizing Curvature: Radius and Concavity
-
Radius of Curvature: This refers to the radius of the circle that best approximates the curve at a given point. A smaller radius of curvature indicates tighter curvature.
-
Concavity: This describes whether a curve is bending upwards (concave up) or downwards (concave down). Understanding concavity is essential in analyzing the behavior of functions and their derivatives.
Curves in Different Contexts
-
Architecture and Design: Curves are aesthetically pleasing and enhance functionality. They are used in building design, furniture design, and even urban planning.
-
Engineering: Curves are incorporated into bridges, roads, and roller coasters to optimize safety and provide a smooth ride.
-
Computer Graphics and Animation: Curves are fundamental in creating realistic images and animations, used to model objects and create smooth transitions.
-
Medical Imaging: Medical scans often utilize curves to represent various anatomical structures. Analyzing these curves aids in diagnosis.
Integrating Slopes and Curves: Advanced Spatial Visualization Techniques
Combining the understanding of slopes and curves unlocks a deeper level of spatial visualization. This involves visualizing how slopes change along a curve, understanding rates of change, and applying these concepts to complex scenarios.
Tangents and Curvature: A Unified Perspective
Consider the relationship between the tangent to a curve and its curvature. The tangent's slope indicates the instantaneous direction of the curve, while the curvature reflects how much the direction changes. Visualizing this interplay is crucial for understanding complex shapes.
Applications in Calculus: Rates of Change
Calculus provides the mathematical tools for precisely analyzing slopes and curves. Derivatives represent the instantaneous rate of change, allowing for the precise calculation of slopes and curvatures at any point on a curve. Integrals are used to calculate areas under curves, representing accumulated change.
3D Spatial Visualization: Extending the Concepts
Extending the concepts of slopes and curves to three dimensions involves visualizing surfaces and their gradients. Imagine a mountain range – the slope at any point on the surface can be represented by a vector, and the overall shape is a complex interplay of curves and slopes in three dimensions.
Exercises and Techniques for Improving Spatial Visualization
Improving your spatial visualization skills requires dedicated practice and the use of specific techniques.
Drawing and Sketching: Visualizing in Action
Regular sketching of slopes and curves, even simple ones, significantly enhances your ability to mentally manipulate them. Start with simple lines, progress to parabolas and circles, and then try more complex curves.
Manipulating Physical Objects: Hands-On Learning
Use physical objects like building blocks or clay to create models of slopes and curves. Manipulate these models to visualize how changes in slope or curvature affect the overall shape.
Using Software and Apps: Interactive Exploration
Several software applications and apps offer interactive tools for exploring slopes and curves. These can provide visual feedback and allow for experimentation with different shapes.
Mental Rotation: Improving Your Internal Imagery
Practice mentally rotating objects in your mind. This exercise strengthens your ability to visualize objects from different perspectives and understand their three-dimensional structure.
Conclusion: The Power of Spatial Visualization
Mastering spatial visualization, particularly concerning slopes and curves, is a skill with widespread applications. It's a crucial component of success in STEM fields, design, and numerous other disciplines. By understanding the fundamental concepts, utilizing practice exercises, and leveraging available tools, you can significantly improve your spatial reasoning abilities and unlock new levels of comprehension and creativity. The continuous development of these skills will undoubtedly benefit you in both professional and personal endeavors.
Latest Posts
Latest Posts
-
Summary For Chapter 11 To Kill A Mockingbird
Mar 31, 2025
-
Which Drive Is Displayed First In The Command Window
Mar 31, 2025
-
Which Of The Following Diagrams Involves A Virtual Image
Mar 31, 2025
-
Which Of The Following Statements About Gerrymandering Is True
Mar 31, 2025
-
9 08 Quiz Act 3 Session 3
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Spatial Vis Slopes And Curves Answers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
