Special Right Triangles Practice 8 3
Onlines
Apr 01, 2025 · 6 min read
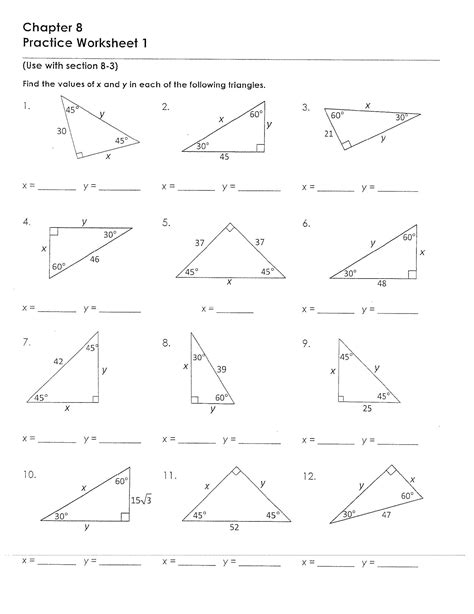
Table of Contents
Special Right Triangles Practice: Mastering 8-3-7 Triangles and Beyond
Special right triangles, those possessing specific angles and side ratios, are fundamental concepts in geometry and trigonometry. Understanding them unlocks efficient problem-solving strategies for a wide range of applications. This comprehensive guide dives deep into special right triangles, focusing on the 8-3-7 triangle (a less common, but still valuable, example) and solidifying your understanding through practice problems and strategies. We'll move beyond simple memorization to build a deep, intuitive grasp of these geometric marvels.
Understanding Special Right Triangles
Before diving into the specifics of 8-3-7 triangles, let's review the most commonly encountered special right triangles:
The 45-45-90 Triangle (Isosceles Right Triangle)
This triangle is characterized by two equal angles (45°) and a right angle (90°). Its sides follow a simple ratio: 1 : 1 : √2. This means that if the legs (the two shorter sides) have length 'x', the hypotenuse (the side opposite the right angle) has length 'x√2'.
The 30-60-90 Triangle (Half of an Equilateral Triangle)
This triangle is formed by bisecting an equilateral triangle. Its side ratios are: 1 : √3 : 2. The shortest side (opposite the 30° angle) is 'x', the side opposite the 60° angle is 'x√3', and the hypotenuse is '2x'.
Delving into the 8-3-7 Triangle (A Non-Special Case Study)
The 8-3-7 triangle isn't a standard special right triangle because its angles aren't neatly defined by simple ratios. However, it presents a valuable opportunity to apply fundamental trigonometric principles and practice problem-solving techniques relevant to all right triangles. We can explore this triangle to solidify our understanding of the relationship between angles and sides.
Let's assume we have a triangle with sides of length 8, 3, and 7. This is not a right-angled triangle because it does not satisfy the Pythagorean theorem (a² + b² = c²). To make it a right-angled triangle, we would have to modify the lengths of its sides. The Pythagorean theorem would be satisfied if the sides are approximately 8, 5, 9.43 or other similar values.
Calculating Angles and Sides using Trigonometry
Given a right-angled triangle with sides a, b, and hypotenuse c, and an angle θ opposite side 'a':
- Sine (sin θ) = a/c (opposite/hypotenuse)
- Cosine (cos θ) = b/c (adjacent/hypotenuse)
- Tangent (tan θ) = a/b (opposite/adjacent)
These trigonometric functions allow us to determine unknown angles or side lengths if we know at least one angle and one side length. Let's apply this to our 8-3-7 triangle, assuming it were a right triangle. Let's treat it hypothetically as a right triangle to demonstrate principles of solving for triangles.
Hypothetical Example (8-3-7 Triangle as a Right Triangle)
Let's assume the hypotenuse is 8 (longest side) and the other sides are 3 and 7.
-
Identify the Right Angle: To treat it as a right triangle, we need to determine which angle is the right angle.
-
Use the Pythagorean Theorem to Check: Does 3² + 7² = 8²? No (9 + 49 ≠ 64). This confirms that with these side lengths, it isn't a right triangle. To proceed further, we need to modify the triangle's side lengths or use the law of cosines to find the angles without a right angle being present.
-
Solving for Angles using the Law of Cosines: If we had a triangle with sides of length a, b, and c, and the angle C opposite side c, then the Law of Cosines states: c² = a² + b² - 2ab cos(C) We can use this to calculate the angles of our 8, 3, 7 triangle.
-
Calculations with Law of Cosines: This requires a calculator capable of handling inverse cosine calculations. You'd plug in the known side lengths to solve for each angle.
This illustrates the importance of the Pythagorean theorem in identifying right triangles and the applicability of trigonometric functions and the Law of Cosines in solving non-right angled triangles, which includes cases where we want to treat the 8-3-7 triangle as a right-angled triangle. This further enhances our ability to analyze triangles, particularly those not conforming to standard special right triangle ratios.
Practice Problems: Special Right Triangles
Let's test your understanding with a variety of problems:
Problem 1: 45-45-90 Triangle
A square has a diagonal of length 10 cm. Find the length of each side.
Solution:
The diagonal of a square forms two 45-45-90 triangles. Using the ratio 1 : 1 : √2, we have:
x√2 = 10
x = 10/√2 = 5√2 cm
Therefore, each side of the square is 5√2 cm.
Problem 2: 30-60-90 Triangle
The shortest side of a 30-60-90 triangle is 6 inches. Find the lengths of the other two sides.
Solution:
Using the ratio 1 : √3 : 2:
Shortest side = x = 6 inches
Side opposite 60° = x√3 = 6√3 inches
Hypotenuse = 2x = 12 inches
Problem 3: Applying Trigonometry to a Non-Special Right Triangle
A right-angled triangle has one leg of length 12 and a hypotenuse of length 13. Find the length of the other leg and the angles (excluding the 90-degree angle).
Solution:
-
Use the Pythagorean Theorem: a² + b² = c²
12² + b² = 13²
144 + b² = 169
b² = 25
b = 5
-
Use Trigonometry to find angles:
sin θ = opposite/hypotenuse = 12/13
θ = arcsin(12/13) ≈ 67.38°
The other angle is 90° - 67.38° ≈ 22.62°
Problem 4: More Complex Scenario
You have a right triangle with a hypotenuse of 10cm and one angle of 35 degrees. Find the lengths of the two legs.
Solution:
-
Use trigonometric functions:
sin(35°) = opposite/hypotenuse => opposite = 10 * sin(35°) ≈ 5.74 cm
cos(35°) = adjacent/hypotenuse => adjacent = 10 * cos(35°) ≈ 8.19 cm
Problem 5: Analyzing a Triangle with Given Sides (Similar to 8-3-7)
Suppose you have a triangle with sides 5, 12, and 13.
Solution: This is a Pythagorean triple (5² + 12² = 13²), therefore, it's a right-angled triangle.
You can calculate the angles using trigonometry as demonstrated in problem 3.
Advanced Concepts and Applications
Mastering special right triangles opens doors to more advanced geometric concepts:
- Trigonometric Identities: Special right triangles are crucial in deriving and understanding trigonometric identities.
- Vectors: Understanding right-angled triangles helps in resolving vectors into their components.
- Calculus: Special right triangles frequently appear in problems involving limits, derivatives, and integrals.
- Three-Dimensional Geometry: These triangles are essential for working with three-dimensional shapes and their properties.
Conclusion: Continued Practice is Key
The journey to mastering special right triangles is one of consistent practice. By working through various problems—from simple applications of the ratios to more complex scenarios involving trigonometry—you'll build a strong intuitive understanding and the ability to efficiently solve problems involving these fundamental geometric shapes. Remember, the 8-3-7 triangle example serves as a valuable reminder that while special right triangles offer shortcuts, the principles of trigonometry and geometric problem-solving remain universally applicable. Continue practicing and expanding your knowledge to tackle more challenging geometric problems effectively.
Latest Posts
Latest Posts
-
When Giving Abdominal Thrusts How Should Brianna Position Her Hands
Apr 02, 2025
-
The Generic Name For Tylenol And Datril Is
Apr 02, 2025
-
Skill Practice 28 Reactions Practice Answers
Apr 02, 2025
-
Which Client Should The Nurse Assess For Degenerative Neurologic Symptoms
Apr 02, 2025
-
Time Phased Activation Might Be Appropriate For
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Special Right Triangles Practice 8 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
