The Set Of Odd Whole Numbers Less Than 24
Onlines
May 10, 2025 · 5 min read
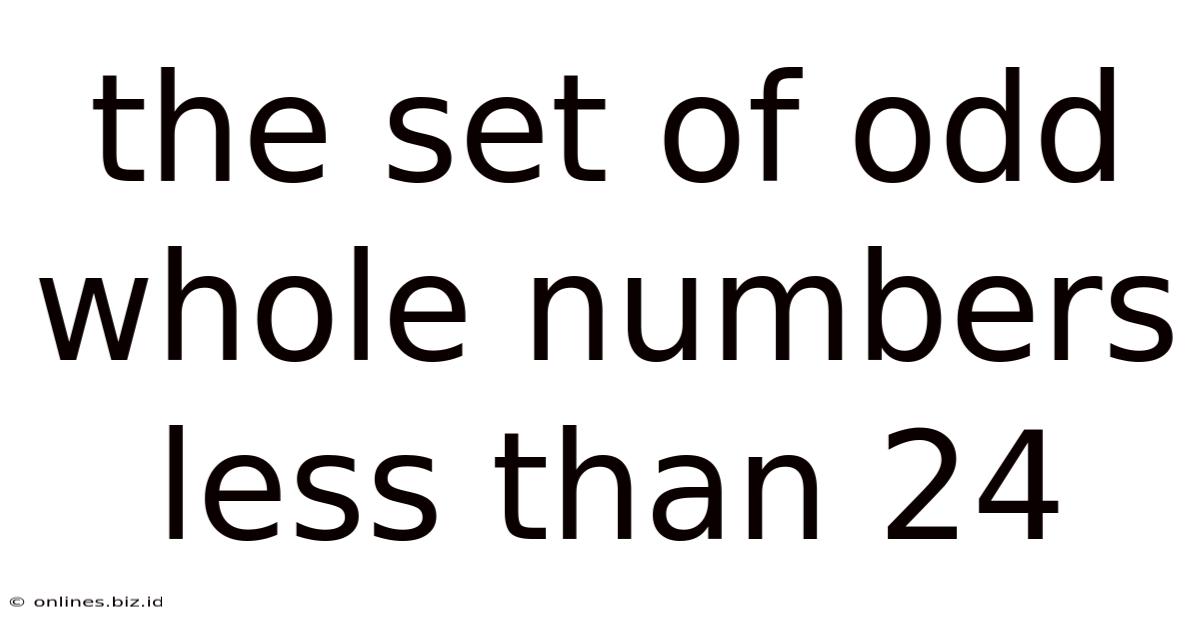
Table of Contents
Delving Deep into the Set of Odd Whole Numbers Less Than 24
The seemingly simple set of odd whole numbers less than 24 – {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23} – offers a surprisingly rich landscape for mathematical exploration. This seemingly small set allows us to explore fundamental concepts in number theory, set theory, and even introduce elementary ideas from more advanced fields. Let's embark on a journey to understand this set comprehensively, touching upon its properties, applications, and connections to broader mathematical ideas.
Defining the Set and its Properties
Our central focus is the set S = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23}. This set is comprised of all positive odd integers strictly less than 24. Several key properties immediately stand out:
1. Finite Set:
This is a finite set, meaning it contains a limited number of elements. Specifically, it has 12 elements. This contrasts with infinite sets like the set of all odd numbers, which extends infinitely.
2. Subset of Natural Numbers:
S is a subset of the natural numbers (denoted by ℕ), which is the set of all positive integers {1, 2, 3, ...}. It's a proper subset because it doesn't include all natural numbers.
3. Arithmetic Progression:
The elements of S form an arithmetic progression with a common difference of 2. An arithmetic progression is a sequence where each term is obtained by adding a constant value (in this case, 2) to the previous term. This property makes it easy to generate the set and predict its elements.
4. Sum of Elements:
The sum of the elements in S can be calculated using the formula for the sum of an arithmetic series: S<sub>n</sub> = n/2 * [2a + (n-1)d], where 'n' is the number of terms, 'a' is the first term, and 'd' is the common difference. In our case, n = 12, a = 1, and d = 2. Therefore, the sum is 12/2 * [2(1) + (12-1)2] = 6 * [2 + 22] = 6 * 24 = 144.
5. Average of Elements:
The average of the elements in S is simply the sum divided by the number of elements: 144 / 12 = 12. Notice that the average is the midpoint of the set.
Exploring Mathematical Operations within the Set
Let's explore some mathematical operations we can perform within this set:
1. Addition and Subtraction:
Adding or subtracting any two elements from S will result in an even number or another element from a different set. For example, 3 + 5 = 8 (even), 11 - 7 = 4 (even), 19 + 3 = 22 (even). But 23 + 1 = 24 (even and not in the set). This illustrates the relationship between odd and even numbers under addition and subtraction.
2. Multiplication:
Multiplying two elements from S will always result in an odd number, but not necessarily one that is within the set S. For example, 3 x 5 = 15 (in S), but 7 x 9 = 63 (not in S).
3. Divisibility:
The elements of S exhibit various divisibility properties. Some are prime numbers (only divisible by 1 and themselves), while others are composite (have more than two factors). Exploring the prime factorization of each element reveals interesting patterns related to the distribution of prime numbers. For example:
- Prime Numbers: 3, 5, 7, 11, 13, 17, 19, 23
- Composite Numbers: 9, 15, 21
Connecting to Broader Mathematical Concepts
The seemingly simple set S provides a springboard to explore several more advanced mathematical concepts:
1. Number Theory:
The set S is intimately tied to number theory. Analyzing the distribution of prime numbers within S, their relative density, and other properties, forms a fundamental aspect of number theory. The study of prime numbers and their distribution is a continuing area of active research.
2. Set Theory:
S demonstrates basic set theory concepts: subsets, finite sets, operations on sets (union, intersection), and cardinality (the number of elements in a set). More complex set theory concepts could be explored using S as a foundational example.
3. Combinatorics:
Combinatorics deals with the arrangement and selection of objects. We can apply combinatorics to S by considering questions like: how many subsets of S exist? How many ways can we select a specific number of elements from S? The answers involve binomial coefficients and factorial calculations.
4. Sequences and Series:
S demonstrates the concept of an arithmetic progression, a type of sequence. The sum of the elements in S demonstrates the calculation of an arithmetic series. This connects to the study of series convergence and divergence in calculus.
5. Modular Arithmetic:
Modular arithmetic, where numbers "wrap around" after reaching a certain value (the modulus), is applicable here. Considering the remainders when elements of S are divided by various moduli could lead to interesting patterns and relationships. For instance, all elements in S leave a remainder of 1 when divided by 2 (this is by definition of odd numbers).
Applications and Real-World Examples
Although this set might seem purely theoretical, understanding this set has practical applications:
1. Programming and Algorithms:
Generating the set S, calculating its sum, and performing operations within S are common tasks in programming. Understanding its properties helps in designing efficient algorithms.
2. Data Analysis:
In data analysis, a set of odd numbers might represent a subset of data points with specific characteristics. Understanding the properties of this set could provide insights into the data distribution.
3. Cryptography:
Prime numbers, some of which are present in S, play a vital role in cryptography. The security of many cryptographic systems relies on the difficulty of factoring large composite numbers into their prime components.
Conclusion
The set of odd whole numbers less than 24, although seemingly simple, offers a rich tapestry of mathematical concepts and applications. From basic set theory to advanced number theory, this small set provides a powerful illustrative tool for understanding fundamental mathematical principles and their connections to diverse fields. Its properties – finite nature, arithmetic progression, sum, and average – provide clear insights into number sequences and series. Its applications extend to programming, data analysis, and even cryptography, demonstrating the importance of understanding even seemingly basic mathematical structures. This detailed exploration reveals how even a seemingly simple mathematical object can provide a window into a vast and complex world of mathematical concepts. Further investigation into the prime factorization, divisibility rules, and advanced applications of this set could lead to a deeper appreciation of its significance.
Latest Posts
Latest Posts
-
Which Statement Best Describes Mary Shelley As A Child
May 10, 2025
-
Where Should An Organizations Web Server Be Placed
May 10, 2025
-
Choose All True Statements About The Activity Of Mpf
May 10, 2025
-
How Can People Boost Their Credibility When Delivering Bad News
May 10, 2025
-
At Appliance City You Sold A Refrigerator
May 10, 2025
Related Post
Thank you for visiting our website which covers about The Set Of Odd Whole Numbers Less Than 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.