Unit 10 Homework 7 Arc And Angle Measures Answers
Onlines
Apr 06, 2025 · 6 min read
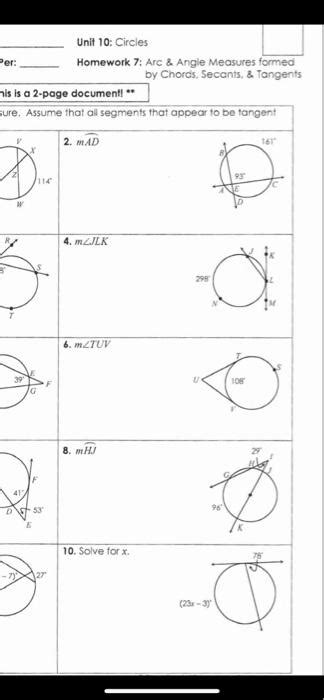
Table of Contents
Unit 10 Homework 7: Arc and Angle Measures - Answers and Comprehensive Guide
This comprehensive guide provides detailed answers and explanations for Unit 10, Homework 7, focusing on arc and angle measures. We'll cover key concepts, theorems, and problem-solving strategies to help you master this crucial geometry topic. Remember, understanding the underlying principles is more important than simply memorizing answers. This guide aims to build your understanding, not just provide solutions.
Understanding Key Concepts: Arcs and Angles in Circles
Before diving into the specific homework problems, let's solidify our understanding of the fundamental concepts:
1. Arcs:
- Arc: A portion of the circumference of a circle. Arcs are measured in degrees, with the entire circumference representing 360 degrees.
- Types of Arcs:
- Minor Arc: An arc less than 180 degrees. It's named by its endpoints (e.g., arc AB).
- Major Arc: An arc greater than 180 degrees. It's named by its endpoints and a point on the arc (e.g., arc ACB).
- Semicircle: An arc that measures exactly 180 degrees.
2. Angles Related to Circles:
- Central Angle: An angle whose vertex is at the center of the circle. The measure of a central angle is equal to the measure of its intercepted arc.
- Inscribed Angle: An angle whose vertex is on the circle and whose sides are chords of the circle. The measure of an inscribed angle is half the measure of its intercepted arc.
- Angle Formed by a Tangent and a Chord: The measure of an angle formed by a tangent and a chord that intersect at a point on the circle is half the measure of the intercepted arc.
- Angle Formed by Two Chords: The measure of an angle formed by two chords intersecting inside a circle is half the sum of the measures of the intercepted arcs.
- Angle Formed by Two Secants, Two Tangents, or a Secant and a Tangent: These angles are formed outside the circle. Their measure is half the difference of the measures of the intercepted arcs.
Problem-Solving Strategies and Examples
Now, let's apply these concepts to solve typical problems found in Unit 10, Homework 7. Since the specific problems aren't provided, we'll tackle various examples encompassing the different angle and arc relationships.
Example 1: Finding the Arc Measure Given a Central Angle
Problem: A central angle in a circle measures 70 degrees. What is the measure of its intercepted arc?
Solution: The measure of a central angle is equal to the measure of its intercepted arc. Therefore, the intercepted arc also measures 70 degrees.
Example 2: Finding the Inscribed Angle Given the Intercepted Arc
Problem: An inscribed angle intercepts an arc measuring 100 degrees. What is the measure of the inscribed angle?
Solution: The measure of an inscribed angle is half the measure of its intercepted arc. Therefore, the inscribed angle measures 100/2 = 50 degrees.
Example 3: Finding the Arc Measure Given an Inscribed Angle
Problem: An inscribed angle measures 35 degrees. What is the measure of its intercepted arc?
Solution: The measure of the intercepted arc is twice the measure of the inscribed angle. Therefore, the intercepted arc measures 35 * 2 = 70 degrees.
Example 4: Angle Formed by a Tangent and a Chord
Problem: A tangent and a chord intersect at a point on a circle. The intercepted arc measures 80 degrees. What is the measure of the angle formed by the tangent and the chord?
Solution: The measure of the angle formed by a tangent and a chord is half the measure of the intercepted arc. Therefore, the angle measures 80/2 = 40 degrees.
Example 5: Angle Formed by Two Chords
Problem: Two chords intersect inside a circle. The intercepted arcs measure 60 degrees and 80 degrees. What is the measure of the angle formed by the chords?
Solution: The measure of the angle formed by two chords intersecting inside a circle is half the sum of the measures of the intercepted arcs. Therefore, the angle measures (60 + 80)/2 = 70 degrees.
Example 6: Angle Formed by Two Secants
Problem: Two secants intersect outside a circle. The intercepted arcs measure 120 degrees and 40 degrees. What is the measure of the angle formed by the secants?
Solution: The measure of the angle formed by two secants intersecting outside a circle is half the difference of the measures of the intercepted arcs. Therefore, the angle measures (120 - 40)/2 = 40 degrees.
Example 7: Problem Involving Multiple Angles and Arcs
Problem: In a circle, a central angle measures 110 degrees. An inscribed angle intercepts the same arc as the central angle. A second inscribed angle intercepts a different arc, and this second inscribed angle measures 25 degrees. Find the measure of the arc intercepted by the second inscribed angle.
Solution:
- Central Angle: The central angle measures 110 degrees; therefore, the arc it intercepts also measures 110 degrees.
- First Inscribed Angle: The first inscribed angle intercepts the same 110-degree arc. Since an inscribed angle is half the measure of its intercepted arc, we know nothing new here.
- Second Inscribed Angle: The second inscribed angle measures 25 degrees. The measure of its intercepted arc is twice this measure (25 degrees * 2 = 50 degrees). Therefore the second arc measures 50 degrees.
Example 8: A More Complex Scenario
Imagine a circle with several chords and tangents. You might be given the measure of some angles and arcs, and asked to find others. The key is to systematically identify the relationships between the given angles and arcs and the unknown ones. Use the theorems discussed earlier to form equations. Often, you’ll need to solve a system of equations to find the solution. For instance, you might find you need to find the measure of a missing arc to solve for the angle.
Tips for Success
- Draw Diagrams: Always start by drawing a clear diagram of the problem. This helps you visualize the relationships between angles and arcs.
- Label Everything: Label all angles and arcs with their known measures. This helps avoid confusion.
- Identify Relationships: Carefully determine which theorems apply to each part of the problem.
- Solve Systematically: Work through the problem step by step, using the relationships you've identified.
- Check Your Answers: Once you have a solution, check to make sure it makes sense in the context of the problem. Do the angle and arc measures add up correctly?
This comprehensive guide provides a foundation for understanding and solving problems related to arc and angle measures in circles. Remember to practice consistently, applying the theorems and strategies discussed here. The more problems you solve, the more confident you’ll become in mastering this important geometric concept. Good luck with your homework!
Latest Posts
Latest Posts
-
Mr Polanski Likes The Cost Of An Hmo Plan
Apr 06, 2025
-
The Diagram That Follows Shows The Market For Agricultural Products
Apr 06, 2025
-
Which Of These Cellular Technologies Offers The Fastest Speeds
Apr 06, 2025
-
Unit 7 Polynomials And Factoring Homework 7 Answer Key
Apr 06, 2025
-
The Love Hypothesis Chapter 16 Adam Pov Read Online Free
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Unit 10 Homework 7 Arc And Angle Measures Answers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
