Unit 2 Linear Functions Homework 2 Standard And Slope-intercept Form
Onlines
Apr 01, 2025 · 6 min read
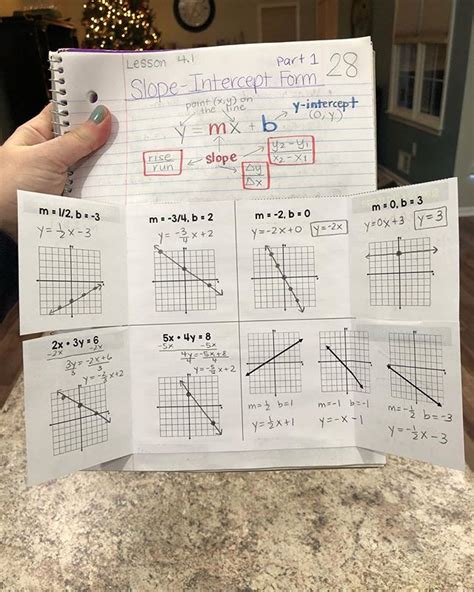
Table of Contents
Unit 2 Linear Functions Homework 2: Mastering Standard and Slope-Intercept Forms
This comprehensive guide delves into the intricacies of linear functions, specifically focusing on standard and slope-intercept forms. We'll tackle common homework problems, providing clear explanations, practical examples, and helpful tips to solidify your understanding. By the end, you'll be confident in converting between forms, graphing linear equations, and interpreting their meaning.
Understanding Linear Functions
Before diving into the different forms, let's establish a strong foundation. A linear function represents a straight line on a graph. It describes a relationship where a constant change in one variable results in a constant change in the other. This constant rate of change is known as the slope.
The general form of a linear equation is:
Ax + By = C
Where:
- 'A', 'B', and 'C' are constants (numbers).
- 'x' and 'y' are variables.
This is often called the standard form. However, there are other forms that offer unique advantages depending on the problem.
Slope-Intercept Form: y = mx + b
The slope-intercept form, y = mx + b, is arguably the most useful form for understanding and graphing linear functions. Let's break down its components:
-
m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward trend (from left to right), while a negative slope indicates a downward trend. A slope of zero signifies a horizontal line, and an undefined slope indicates a vertical line. The slope is calculated as the change in 'y' divided by the change in 'x':
m = (y₂ - y₁) / (x₂ - x₁). -
b: Represents the y-intercept. This is the point where the line crosses the y-axis (where x = 0). It's the value of 'y' when 'x' is zero.
Example: Graphing from Slope-Intercept Form
Let's graph the equation y = 2x + 3.
-
Identify the slope (m) and y-intercept (b): In this equation, m = 2 and b = 3.
-
Plot the y-intercept: Start by plotting the point (0, 3) on the y-axis.
-
Use the slope to find another point: The slope is 2, which can be expressed as 2/1. This means that for every 1-unit increase in x, y increases by 2 units. Starting from (0, 3), move 1 unit to the right and 2 units up. This gives you the point (1, 5).
-
Draw the line: Draw a straight line through the points (0, 3) and (1, 5). This line represents the equation
y = 2x + 3.
Example: Finding the Equation from Points
Suppose you have two points, (1, 4) and (3, 10). How do you find the equation in slope-intercept form?
-
Calculate the slope:
m = (10 - 4) / (3 - 1) = 6 / 2 = 3 -
Use the point-slope form: The point-slope form is
y - y₁ = m(x - x₁), where (x₁, y₁) is one of the points. Let's use (1, 4):y - 4 = 3(x - 1) -
Solve for y:
y - 4 = 3x - 3y = 3x + 1
This is the equation in slope-intercept form.
Standard Form: Ax + By = C
The standard form, Ax + By = C, is particularly useful when dealing with systems of equations or when you need to find intercepts easily.
- 'A', 'B', and 'C' are integers (whole numbers). It's customary to have 'A' as a positive integer.
Example: Converting from Slope-Intercept to Standard Form
Let's convert the equation y = 2x + 3 (from the previous example) to standard form.
-
Subtract 2x from both sides:
-2x + y = 3 -
Multiply by -1 to make 'A' positive:
2x - y = -3
Now the equation is in standard form.
Example: Finding Intercepts from Standard Form
To find the x-intercept (where the line crosses the x-axis, y = 0), set y = 0 and solve for x. To find the y-intercept (where the line crosses the y-axis, x = 0), set x = 0 and solve for y.
Let's use the equation 2x - y = -3.
-
x-intercept: Set y = 0:
2x - 0 = -3 => x = -3/2The x-intercept is (-3/2, 0). -
y-intercept: Set x = 0:
2(0) - y = -3 => y = 3The y-intercept is (0, 3).
Converting Between Forms
The ability to seamlessly convert between slope-intercept and standard forms is crucial. Here's a summary of the conversion process:
Slope-Intercept to Standard Form:
- Move the 'x' term to the left side of the equation.
- Ensure 'A' is a positive integer by multiplying both sides by -1 if necessary.
Standard Form to Slope-Intercept Form:
- Solve the equation for 'y'. Isolate 'y' on one side of the equation.
- The coefficient of 'x' is the slope (m), and the constant term is the y-intercept (b).
Parallel and Perpendicular Lines
Understanding the relationship between slopes of parallel and perpendicular lines is essential.
-
Parallel Lines: Parallel lines have the same slope but different y-intercepts.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. If the slope of one line is 'm', the slope of the perpendicular line is '-1/m'.
Word Problems and Real-World Applications
Linear functions are not confined to theoretical exercises; they have numerous real-world applications. Word problems often test your ability to translate real-world scenarios into linear equations.
Example: A taxi charges a $3 initial fee plus $2 per mile. Write a linear equation representing the total cost (y) based on the number of miles (x).
The equation would be: y = 2x + 3. This is directly in slope-intercept form, where the slope (2) represents the cost per mile, and the y-intercept (3) represents the initial fee.
Advanced Concepts and Further Exploration
Once you've mastered the basics, you can explore more advanced concepts related to linear functions, including:
- Systems of Linear Equations: Solving for the point of intersection of two or more lines.
- Linear Inequalities: Representing regions on a graph rather than just lines.
- Applications in Calculus: Understanding linear approximation and tangent lines.
Practice Makes Perfect
The key to mastering linear functions is consistent practice. Work through numerous problems, varying the types of questions and the forms used. Don't be afraid to seek help when needed. Utilize online resources, tutoring services, or ask your teacher for clarification on any confusing concepts.
Conclusion
Understanding the standard and slope-intercept forms of linear functions is a fundamental building block in algebra and beyond. By mastering these concepts and practicing regularly, you'll build a strong foundation for more advanced mathematical concepts and be able to apply these skills to solve a wide range of real-world problems. Remember to break down complex problems into smaller, manageable steps, and always double-check your work. Good luck with your homework!
Latest Posts
Latest Posts
-
Regardless Of Where Portable And Mounted Oxygen
Apr 02, 2025
-
Student Exploration Building Pangaea Answer Key
Apr 02, 2025
-
All Of The Following Would Be Considered Unprofessional Conduct Except
Apr 02, 2025
-
Identify The True And False Statements About Within Groups Designs
Apr 02, 2025
-
An Example Of Enamel Bonding Is The Placement Of A
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Unit 2 Linear Functions Homework 2 Standard And Slope-intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
