Unit 3 Power Polynomials And Rational Functions
Onlines
Apr 03, 2025 · 6 min read
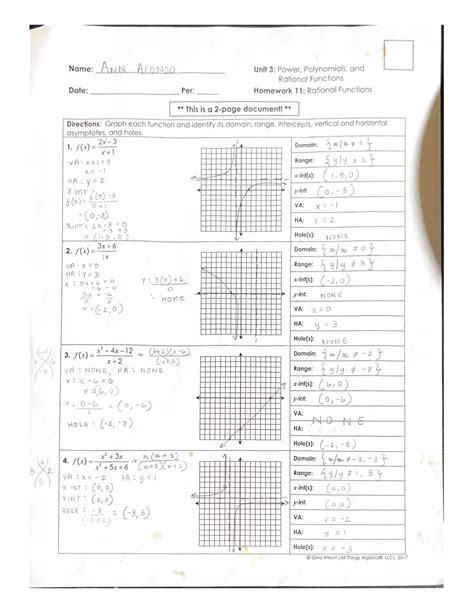
Table of Contents
Unit 3: Power Polynomials and Rational Functions: A Comprehensive Guide
This unit delves into the fascinating world of power polynomials and rational functions, exploring their properties, graphs, and applications. We'll cover key concepts, problem-solving techniques, and real-world examples to solidify your understanding.
Understanding Power Polynomials
Power polynomials, a subset of polynomial functions, are defined by a single term containing a variable raised to a power. They take the form:
f(x) = ax<sup>n</sup>
where:
ais a non-zero constant (the coefficient).xis the variable.nis a non-negative integer (the exponent or degree).
Key Properties of Power Polynomials
- Domain: The domain of a power polynomial is all real numbers, (-∞, ∞). This means you can substitute any real number for x and get a real number output.
- Range: The range depends on the degree (n) and the coefficient (a).
- If n is even and a is positive, the range is [0, ∞).
- If n is even and a is negative, the range is (-∞, 0].
- If n is odd, the range is (-∞, ∞).
- Symmetry: Power polynomials exhibit symmetry depending on the exponent.
- If n is even, the function is symmetric about the y-axis (even function).
- If n is odd, the function is symmetric about the origin (odd function).
- End Behavior: The end behavior describes what happens to the function's values as x approaches positive or negative infinity. This is heavily influenced by the degree (n) and the coefficient (a).
Graphing Power Polynomials
Graphing power polynomials is relatively straightforward. Key features to consider include:
- x-intercept: The x-intercept is always at (0, 0) unless a horizontal shift is applied.
- y-intercept: The y-intercept is always at (0, 0).
- Symmetry: Utilize the symmetry properties discussed above to aid in sketching.
- End Behavior: Consider the end behavior to determine the overall shape of the graph.
Example: Let's graph f(x) = 2x³.
This is a power polynomial with a = 2 and n = 3.
- It's an odd function, symmetric about the origin.
- Its range is (-∞, ∞).
- As x → ∞, f(x) → ∞.
- As x → -∞, f(x) → -∞.
The graph will pass through the origin (0, 0) and increase monotonically.
Delving into Rational Functions
Rational functions are defined as the ratio of two polynomial functions:
f(x) = p(x) / q(x)
where:
- p(x) and q(x) are polynomial functions.
- q(x) ≠ 0 (the denominator cannot be zero).
Key Characteristics of Rational Functions
- Domain: The domain of a rational function is all real numbers except for the values of x that make the denominator equal to zero. These values are called vertical asymptotes.
- Range: The range is more complex and depends on the degrees of p(x) and q(x) and the presence of horizontal asymptotes.
- Asymptotes: Rational functions can have vertical, horizontal, and oblique (slant) asymptotes.
- Vertical Asymptotes: Occur where the denominator is zero and the numerator is non-zero.
- Horizontal Asymptotes: Determined by comparing the degrees of the numerator and denominator.
- If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
- If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is y = (leading coefficient of numerator) / (leading coefficient of denominator).
- If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote, but there might be an oblique asymptote.
- Oblique Asymptotes: Occur when the degree of the numerator is exactly one greater than the degree of the denominator. They are found using polynomial long division.
- x-intercepts: Found by setting the numerator equal to zero and solving for x, provided the denominator is not also zero at that point.
- y-intercepts: Found by evaluating f(0), provided that f(0) is defined.
Graphing Rational Functions
Graphing rational functions requires a systematic approach:
- Find the domain: Identify any vertical asymptotes.
- Find the intercepts: Determine the x- and y-intercepts.
- Find the asymptotes: Identify horizontal or oblique asymptotes.
- Analyze the behavior near asymptotes: Determine whether the function approaches the asymptote from above or below.
- Plot points: Choose additional points to refine the graph's shape.
Example: Let's graph f(x) = (x + 1) / (x - 2)
- Domain: x ≠ 2 (vertical asymptote at x = 2).
- Intercepts: x-intercept at x = -1, y-intercept at y = -1/2.
- Asymptotes: Horizontal asymptote at y = 1 (degrees of numerator and denominator are equal).
- Behavior near asymptotes: As x approaches 2 from the left, f(x) approaches -∞. As x approaches 2 from the right, f(x) approaches ∞.
- Plot points: Choose additional points to complete the graph.
Applications of Power Polynomials and Rational Functions
Power polynomials and rational functions have numerous real-world applications:
Power Polynomials Applications:
- Physics: Modeling projectile motion, calculating energy, and describing the relationship between variables in various physical phenomena. For example, the distance an object falls under gravity is modeled by a power polynomial.
- Engineering: Designing structures, analyzing stresses and strains, and modeling the behavior of systems.
- Economics: Representing growth curves, modeling market trends, and analyzing economic indicators.
- Computer Graphics: Creating curves and shapes in computer-aided design (CAD) software.
Rational Functions Applications:
- Physics: Describing inverse square laws (e.g., gravity and electromagnetism).
- Chemistry: Modeling reaction rates and concentrations.
- Engineering: Analyzing electrical circuits and control systems. Rational functions are frequently employed in transfer functions within control theory.
- Economics: Modeling supply and demand curves and analyzing marginal costs and revenue.
Solving Problems Involving Power Polynomials and Rational Functions
Problem-solving often involves manipulating these functions algebraically, finding intercepts and asymptotes, and sketching graphs. Here are some common problem types:
- Finding the domain and range: Requires identifying restrictions on the variable (for rational functions) and understanding the behavior of the function.
- Finding intercepts: Involves setting the function equal to zero (for x-intercepts) or substituting x = 0 (for y-intercepts).
- Determining asymptotes: Requires comparing the degrees of the numerator and denominator (for rational functions) and performing polynomial long division if needed.
- Sketching graphs: Combines all of the above information to produce an accurate visual representation of the function.
- Solving equations involving rational functions: Might involve simplifying complex rational expressions, finding a common denominator, and solving for the unknown variable.
Advanced Topics
Further exploration of power polynomials and rational functions could include:
- Partial Fraction Decomposition: A technique for breaking down complex rational functions into simpler fractions, useful in calculus and other advanced applications.
- Polynomial Long Division: A crucial technique for simplifying rational functions and finding oblique asymptotes.
- Transformations of Functions: Understanding how shifting, stretching, and reflecting the graph of a power polynomial or rational function impacts its equation.
Conclusion
This comprehensive guide provides a solid foundation for understanding power polynomials and rational functions. Mastering these concepts is essential for success in various mathematical and scientific fields. By understanding their properties, graphs, and applications, you can effectively solve problems and apply this knowledge to a wide range of real-world scenarios. Remember to practice regularly and explore the advanced topics to solidify your understanding and enhance your problem-solving abilities. This deep dive into the subject ensures a thorough comprehension, laying the groundwork for further mathematical exploration.
Latest Posts
Latest Posts
-
Characters In Hound Of The Baskervilles
Apr 04, 2025
-
Risk Management For Small Unit Leaders Pre Test
Apr 04, 2025
-
Wide Sargasso Sea Part 1 Summary
Apr 04, 2025
-
Chapter 13 Things Fall Apart Summary
Apr 04, 2025
-
Answers To Laboratory Manual For Anatomy And Physiology
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Unit 3 Power Polynomials And Rational Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
