Unit 5 Polynomial Functions Homework 2 Answer Key
Onlines
Mar 30, 2025 · 6 min read
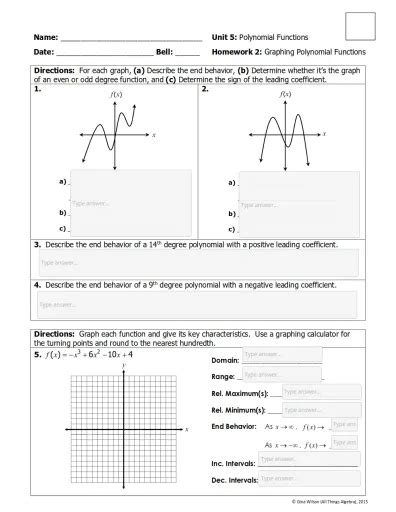
Table of Contents
Unit 5 Polynomial Functions Homework 2 Answer Key: A Comprehensive Guide
Finding a reliable answer key for your Unit 5 Polynomial Functions Homework 2 can be tricky. Many students struggle with the complexities of polynomials, from identifying their degree and leading coefficient to understanding end behavior and applying the Remainder and Factor Theorems. This comprehensive guide aims to provide clarity and understanding, helping you not just find the answers, but also master the underlying concepts. We'll delve into various polynomial function problems, offering detailed explanations and solutions that will boost your confidence and improve your problem-solving skills. Remember, understanding why you arrive at an answer is far more valuable than just knowing the answer itself.
Note: This guide provides a framework and examples. Specific problem numbers and exact wording will vary depending on your textbook and curriculum. Use this as a guide to understand the concepts and solve your specific homework problems. Always refer back to your textbook and class notes for clarification.
Section 1: Fundamental Concepts of Polynomial Functions
Before we dive into specific problems, let's refresh some crucial concepts:
-
Polynomial Function Definition: A polynomial function is a function that can be expressed in the form:
f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0, where 'n' is a non-negative integer (the degree of the polynomial), and the 'a_i' are constants (coefficients). -
Degree of a Polynomial: The highest power of x in the polynomial. This determines the number of roots (or zeros) the polynomial has.
-
Leading Coefficient: The coefficient of the term with the highest power of x. This influences the end behavior of the polynomial.
-
Roots/Zeros: The values of x for which f(x) = 0. These are where the graph intersects the x-axis.
-
End Behavior: How the graph behaves as x approaches positive and negative infinity. It's determined by the degree and leading coefficient.
-
Remainder Theorem: When a polynomial f(x) is divided by (x-c), the remainder is f(c).
-
Factor Theorem: (x-c) is a factor of f(x) if and only if f(c) = 0.
Section 2: Sample Problems and Solutions
Let's tackle some typical problems encountered in a Unit 5 Polynomial Functions Homework 2 assignment. Remember to always show your work; this helps you identify errors and demonstrates your understanding to your teacher.
Problem 1: Identifying Polynomial Characteristics
Question: Consider the polynomial function f(x) = 3x⁴ - 2x³ + 5x - 7.
(a) What is the degree of the polynomial? (b) What is the leading coefficient? (c) Describe the end behavior of the function.
Solution:
(a) The degree of the polynomial is 4 (the highest power of x).
(b) The leading coefficient is 3 (the coefficient of x⁴).
(c) Since the degree is even (4) and the leading coefficient is positive (3), the end behavior is: as x → ∞, f(x) → ∞; and as x → -∞, f(x) → ∞. The graph rises on both ends.
Problem 2: Finding Roots (Zeros) of a Polynomial
Question: Find the roots of the polynomial function g(x) = x³ - 6x² + 11x - 6.
Solution: This cubic polynomial can be factored. We look for factors of -6 that add up to -6 (the coefficient of x²). Through trial and error (or using the Rational Root Theorem), we find that (x-1), (x-2), and (x-3) are factors. Therefore:
g(x) = (x - 1)(x - 2)(x - 3)
The roots (zeros) are x = 1, x = 2, and x = 3.
Problem 3: Applying the Remainder Theorem
Question: Use the Remainder Theorem to find the remainder when f(x) = 2x³ + 7x² - 5x + 4 is divided by (x + 2).
Solution: The Remainder Theorem states that the remainder is f(-2). Substituting -2 for x:
f(-2) = 2(-2)³ + 7(-2)² - 5(-2) + 4 = -16 + 28 + 10 + 4 = 26
The remainder is 26.
Problem 4: Applying the Factor Theorem
Question: Is (x - 3) a factor of h(x) = x³ - 5x² + 3x + 9?
Solution: According to the Factor Theorem, (x - 3) is a factor if h(3) = 0. Let's evaluate h(3):
h(3) = (3)³ - 5(3)² + 3(3) + 9 = 27 - 45 + 9 + 9 = 0
Since h(3) = 0, (x - 3) is a factor of h(x).
Problem 5: Graphing Polynomial Functions
Question: Sketch the graph of the polynomial function p(x) = -x⁴ + 4x².
Solution: This involves several steps:
-
Find the roots: Factor the polynomial: p(x) = -x²(x² - 4) = -x²(x - 2)(x + 2). The roots are x = 0, x = 2, and x = -2.
-
Determine the end behavior: Since the degree is even (4) and the leading coefficient is negative (-1), the end behavior is: as x → ∞, p(x) → -∞; and as x → -∞, p(x) → -∞. The graph falls on both ends.
-
Determine the multiplicity of roots: The root x = 0 has a multiplicity of 2 (because of x²), meaning the graph touches the x-axis at x = 0 but doesn't cross it. The roots x = 2 and x = -2 have a multiplicity of 1, so the graph crosses the x-axis at these points.
-
Find additional points: Calculate a few additional points (e.g., p(1), p(-1)) to help you sketch the graph accurately.
-
Sketch the graph: Using the information gathered above, you can now accurately sketch the graph of p(x).
Problem 6: Solving Polynomial Inequalities
Question: Solve the inequality x³ - 4x > 0.
Solution:
-
Find the roots: Factor the expression: x(x² - 4) = x(x - 2)(x + 2). The roots are x = 0, x = 2, and x = -2.
-
Test intervals: Test the intervals (-∞, -2), (-2, 0), (0, 2), and (2, ∞) to determine where the expression is positive (greater than 0).
-
Solution: After testing, you'll find that the inequality is true when x ∈ (-2, 0) ∪ (2, ∞).
Section 3: Advanced Polynomial Concepts and Problem Types
Your Unit 5 Polynomial Functions Homework 2 might also include more challenging problems involving:
-
Synthetic Division: A shortcut method for dividing polynomials.
-
Rational Root Theorem: Helps you find possible rational roots of a polynomial.
-
Complex Roots: Understanding that polynomials can have complex (imaginary) roots that come in conjugate pairs.
-
Polynomial Long Division: A more general method for dividing polynomials, applicable even when the divisor is not of the form (x-c).
This guide provides a solid foundation to tackle these advanced problems. Remember to break down each problem into smaller, manageable steps. Consult your textbook, class notes, and online resources for further explanations and practice problems. The key to mastering polynomial functions is consistent practice and a deep understanding of the fundamental concepts.
Section 4: Strategies for Success
Here are some practical strategies to improve your performance on homework and exams:
-
Active Learning: Don't just passively read the material. Actively engage with it by working through examples, taking notes, and asking questions.
-
Practice, Practice, Practice: The more problems you solve, the better you'll understand the concepts.
-
Seek Help When Needed: Don't hesitate to ask your teacher, tutor, or classmates for help when you're stuck.
-
Study Groups: Collaborating with others can enhance your understanding and provide different perspectives.
-
Review Regularly: Regular review helps reinforce concepts and prevents forgetting.
By combining a strong understanding of the underlying concepts with consistent practice and effective study habits, you can confidently conquer your Unit 5 Polynomial Functions Homework 2 and master this important area of mathematics. Remember, it's about understanding the why as much as the what. Good luck!
Latest Posts
Latest Posts
-
The Septic Tank In This Figure Will Probably
Apr 01, 2025
-
Which Choice Best Characterizes K Leakage Channels
Apr 01, 2025
-
This Group Has A Fascination And Fear About Dying
Apr 01, 2025
-
Six Kingdoms Coloring Worksheet Answer Key
Apr 01, 2025
-
A Peoples History Of The United States Summary Chapter 1
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Unit 5 Polynomial Functions Homework 2 Answer Key . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
