Unit 8 Homework 5 Trigonometry Finding Sides And Angles
Onlines
Mar 29, 2025 · 6 min read
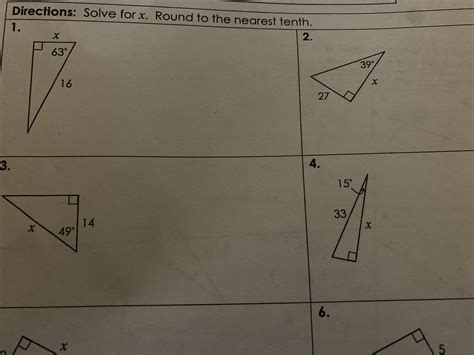
Table of Contents
Unit 8 Homework 5: Trigonometry – Finding Sides and Angles: A Comprehensive Guide
Trigonometry, the study of triangles, is a fundamental branch of mathematics with far-reaching applications in various fields, including engineering, physics, and computer graphics. Unit 8, Homework 5, often focuses on the crucial skill of finding unknown sides and angles within triangles using trigonometric functions. This comprehensive guide will walk you through the essential concepts, formulas, and problem-solving strategies necessary to master this topic. We'll cover right-angled triangles in detail and then briefly touch upon the application of the sine and cosine rules for non-right-angled triangles.
Understanding the Trigonometric Functions (SOH CAH TOA)
The foundation of solving trigonometric problems lies in understanding the three primary trigonometric functions: sine, cosine, and tangent. These functions relate the angles of a right-angled triangle to the ratios of its sides. The mnemonic SOH CAH TOA is incredibly helpful in remembering these relationships:
- SOH: Sine (sin) = Opposite / Hypotenuse
- CAH: Cosine (cos) = Adjacent / Hypotenuse
- TOA: Tangent (tan) = Opposite / Adjacent
Remember:
- Hypotenuse: The longest side of a right-angled triangle, opposite the right angle (90°).
- Opposite: The side opposite the angle you are considering.
- Adjacent: The side next to the angle you are considering (and not the hypotenuse).
Solving Right-Angled Triangles: Finding Sides
When solving for unknown sides in a right-angled triangle, you'll use the appropriate trigonometric function based on the information provided. Let's work through a few examples:
Example 1: Finding the Opposite Side
Let's say we have a right-angled triangle where one angle is 30°, and the hypotenuse is 10 cm. We want to find the length of the side opposite the 30° angle.
- Identify the known values: We know the angle (30°) and the hypotenuse (10 cm).
- Choose the appropriate function: Since we have the hypotenuse and want to find the opposite side, we use the sine function (SOH).
- Set up the equation: sin(30°) = Opposite / 10 cm
- Solve for the opposite side: Opposite = 10 cm * sin(30°) (Remember that sin(30°) = 0.5)
- Calculate: Opposite = 10 cm * 0.5 = 5 cm
Therefore, the length of the opposite side is 5 cm.
Example 2: Finding the Adjacent Side
Consider a right-angled triangle with a 45° angle and an opposite side of 7 cm. We need to determine the adjacent side.
- Identify the known values: We have the angle (45°) and the opposite side (7 cm).
- Choose the appropriate function: Since we know the opposite and need the adjacent, we use the tangent function (TOA).
- Set up the equation: tan(45°) = 7 cm / Adjacent
- Solve for the adjacent side: Adjacent = 7 cm / tan(45°) (Remember that tan(45°) = 1)
- Calculate: Adjacent = 7 cm / 1 = 7 cm
The adjacent side measures 7 cm.
Example 3: Finding the Hypotenuse
Suppose we know the adjacent side (8 cm) and an angle of 60°. We want to calculate the hypotenuse.
- Identify the known values: We have the adjacent side (8 cm) and the angle (60°).
- Choose the appropriate function: We use the cosine function (CAH) since we know the adjacent and need the hypotenuse.
- Set up the equation: cos(60°) = 8 cm / Hypotenuse
- Solve for the hypotenuse: Hypotenuse = 8 cm / cos(60°) (Remember that cos(60°) = 0.5)
- Calculate: Hypotenuse = 8 cm / 0.5 = 16 cm
The length of the hypotenuse is 16 cm.
Solving Right-Angled Triangles: Finding Angles
To find unknown angles in a right-angled triangle, you'll use the inverse trigonometric functions: arcsine (sin⁻¹), arccosine (cos⁻¹), and arctangent (tan⁻¹). These functions give you the angle whose sine, cosine, or tangent is a given value. These are often denoted as asin, acos, and atan on calculators.
Example 4: Finding an Angle using the Opposite and Hypotenuse
Assume we have a right-angled triangle with an opposite side of 6 cm and a hypotenuse of 10 cm. We want to find the angle opposite the 6 cm side.
- Identify the known values: We know the opposite (6 cm) and hypotenuse (10 cm).
- Choose the appropriate function: We'll use the arcsine function because we have the opposite and hypotenuse.
- Set up the equation: Angle = sin⁻¹(6 cm / 10 cm)
- Calculate: Angle = sin⁻¹(0.6) ≈ 36.87°
The angle is approximately 36.87°.
Example 5: Finding an Angle using the Adjacent and Hypotenuse
In a right-angled triangle, the adjacent side is 5 cm and the hypotenuse is 13 cm. Find the angle.
- Identify the known values: Adjacent = 5 cm, Hypotenuse = 13 cm.
- Choose the appropriate function: We use the arccosine function.
- Set up the equation: Angle = cos⁻¹(5 cm / 13 cm)
- Calculate: Angle = cos⁻¹(5/13) ≈ 67.38°
The angle is approximately 67.38°.
Example 6: Finding an Angle using the Opposite and Adjacent
If the opposite side is 4 cm and the adjacent side is 3 cm, determine the angle.
- Identify the known values: Opposite = 4 cm, Adjacent = 3 cm.
- Choose the appropriate function: We use the arctangent function.
- Set up the equation: Angle = tan⁻¹(4 cm / 3 cm)
- Calculate: Angle = tan⁻¹(4/3) ≈ 53.13°
The angle is approximately 53.13°.
Solving Non-Right-Angled Triangles: Sine and Cosine Rules
While SOH CAH TOA works exclusively for right-angled triangles, non-right-angled triangles require the Sine Rule and the Cosine Rule.
The Sine Rule: This rule relates the sides and angles of any triangle. It states:
a / sin(A) = b / sin(B) = c / sin(C)
Where a, b, and c are the lengths of the sides opposite angles A, B, and C respectively.
The Cosine Rule: This rule is useful for finding sides or angles when you have three sides or two sides and the included angle. It has two forms:
- Finding a side: a² = b² + c² - 2bc * cos(A)
- Finding an angle: cos(A) = (b² + c² - a²) / 2bc
Remember to always label your triangles consistently to avoid confusion.
Practical Applications and Further Exploration
Trigonometry is not just a theoretical exercise; it has numerous real-world applications. Consider these examples:
- Surveying: Determining distances and heights using angle measurements.
- Navigation: Calculating distances and directions using GPS and other navigational tools.
- Engineering: Designing structures and calculating forces.
- Physics: Analyzing projectile motion and wave phenomena.
By mastering the concepts and techniques outlined in this guide, you'll be well-equipped to tackle Unit 8 Homework 5 and further expand your understanding of trigonometry. Remember to practice regularly, work through diverse problem types, and utilize online resources and calculators to reinforce your learning. Consistent practice is key to mastering trigonometric calculations and their applications. Don't hesitate to seek help from teachers, tutors, or online communities if you encounter difficulties. The more you practice, the more confident you'll become in solving a wide range of trigonometric problems. Good luck!
Latest Posts
Latest Posts
-
Terri Owns A Computer Repair Shop
Mar 31, 2025
-
Which Of The Following Statements Is True Of Bullying
Mar 31, 2025
-
Please Place The Following Societies In Chronological Order
Mar 31, 2025
-
Un Dia De Primavera Antonio Y Alicia
Mar 31, 2025
-
The Author Most Likely Included This Paragraph To
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Unit 8 Homework 5 Trigonometry Finding Sides And Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
