What Is The Domain Of The Relation Graphed Below
Onlines
Apr 03, 2025 · 5 min read
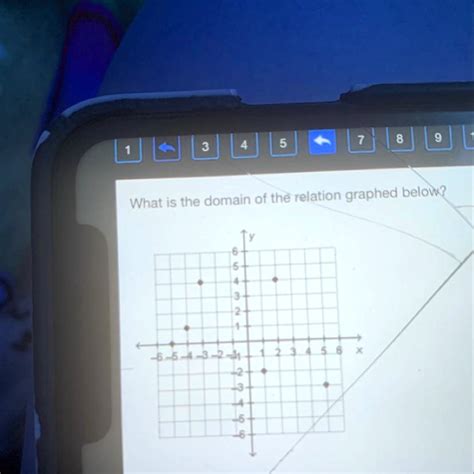
Table of Contents
Decoding Relations: Understanding the Domain of a Graphed Relation
Determining the domain of a relation from its graph is a fundamental concept in mathematics, particularly within the realms of algebra, precalculus, and calculus. Understanding the domain helps us comprehend the limitations and scope of a function or relation. This article will delve deeply into identifying the domain from a graph, exploring various types of relations and offering practical examples to solidify your understanding.
What is a Relation?
Before we dive into the domain, let's define a relation. A relation is simply a set of ordered pairs. Each ordered pair (x, y) connects an input value (x) to an output value (y). The set of all possible input values (x-values) forms the domain, while the set of all possible output values (y-values) forms the range.
Think of a relation as a machine: you input an x-value, and the machine produces a y-value (or possibly multiple y-values). The domain represents all the valid inputs the machine can accept without breaking down.
Visualizing the Domain on a Graph
The beauty of graphing a relation lies in its visual representation. The domain can be easily identified by examining the graph's extent along the x-axis. The domain encompasses all the x-values where the relation is defined.
Identifying the Domain from Different Types of Graphs
Different types of graphs represent relations in unique ways, requiring slightly different approaches to identifying the domain. Let's explore some common graph types:
1. Discrete Relations:
Discrete relations are represented by a set of distinct, unconnected points. To find the domain, simply list the x-coordinates of each point.
Example: If a graph shows points at (1, 2), (3, 4), and (5, 6), the domain is {1, 3, 5}. There are no values of x between 1 and 3, or 3 and 5, that are part of the relation.
2. Continuous Relations:
Continuous relations are represented by unbroken lines or curves. The domain here is typically an interval or a union of intervals.
A) Linear Relations:
Linear relations are represented by straight lines. Unless the line is perfectly vertical, the domain will typically extend infinitely in both directions along the x-axis. This is represented using interval notation as (-∞, ∞). A vertical line, however, has a restricted domain, which we'll address shortly.
B) Polynomial Relations:
Polynomial relations (quadratic, cubic, etc.) are smooth curves. Their domains are usually also (-∞, ∞) because you can plug in any real number into the polynomial equation and get a real number out.
C) Rational Relations:
Rational relations involve fractions where the denominator contains a variable. The domain excludes any x-value that makes the denominator equal to zero, as division by zero is undefined. Identifying these values requires solving the equation in the denominator to find the values to exclude.
Example: Consider the rational function f(x) = 1/(x - 2). The denominator is zero when x = 2. Therefore, the domain is (-∞, 2) U (2, ∞). We use the union symbol (U) to combine the two intervals.
D) Radical Relations (Square Roots and Cube Roots):
For even-indexed roots (square roots, fourth roots, etc.), the expression inside the radical must be non-negative (greater than or equal to zero) for the result to be a real number. For odd-indexed roots (cube roots, fifth roots, etc.), the domain is all real numbers because you can take the cube root (or any odd root) of any number, both positive and negative.
Example: The domain of √(x - 3) is [3, ∞) because x - 3 must be greater than or equal to zero, thus x ≥ 3.
E) Trigonometric Relations:
Trigonometric functions like sine, cosine, and tangent have specific domains. Sine and cosine are defined for all real numbers, resulting in a domain of (-∞, ∞). However, tangent has vertical asymptotes where the cosine is zero, meaning these values must be excluded from the domain.
Example: The tangent function, tan(x), has a domain that excludes all values of x that make cos(x) = 0. These values occur at x = (π/2) + nπ, where n is any integer.
3. Relations with Restricted Domains:
Some relations might have explicitly stated restrictions on the domain. This could be because of context, specific conditions, or practical limitations. The graph would visually show only the values of x within the defined domain. For example, a model might only be valid for a specific range of x-values, such as time or temperature.
Advanced Techniques and Considerations:
-
Piecewise Functions: Piecewise functions have different rules for different parts of their domain. The domain is determined by analyzing the domain of each piece and combining them appropriately.
-
Implicitly Defined Relations: Relations defined implicitly (e.g., x² + y² = 1) require more careful analysis to determine the domain. Often, solving for y in terms of x or using techniques like partial derivatives will be necessary.
-
Using Interval Notation: Always strive to express the domain using appropriate interval notation:
- (a, b): Open interval, excluding a and b.
- [a, b]: Closed interval, including a and b.
- (a, b]: Half-open interval, including b but excluding a.
- [a, b): Half-open interval, including a but excluding b.
- (-∞, a): All real numbers less than a.
- (a, ∞): All real numbers greater than a.
- (-∞, ∞): All real numbers.
Practical Applications:
Understanding the domain is crucial in various applications:
-
Modeling Real-World Phenomena: Models often have limitations, such as temperature ranges or feasible values for variables, which are reflected in their domains.
-
Data Analysis: Identifying the domain helps understand the range of data available and any potential limitations.
-
Computer Programming: The domain helps define the valid input values for a function, preventing errors and ensuring reliable performance.
-
Engineering and Physics: Models used to describe physical systems have constrained domains to accurately reflect the limits of those systems.
Conclusion:
Identifying the domain of a graphed relation is a fundamental skill that underpins many areas of mathematics and its applications. By systematically examining the graph along the x-axis, considering the type of relation, and employing interval notation, you can confidently determine the domain and understand the limits of the relation you are working with. Remember to always consider the context of the problem and any explicit restrictions that may apply. This thorough understanding allows for a deeper grasp of the relationships between variables and empowers more accurate and effective problem-solving across numerous disciplines.
Latest Posts
Latest Posts
-
Which Of The Following Is The Best Example Of Cogeneration
Apr 04, 2025
-
What Are Two More Purposes Of The Violent Incident Log
Apr 04, 2025
-
Kumon Answer Book Pdf Level D
Apr 04, 2025
-
Select The Social Media Site That Is An Idea Sharing Website
Apr 04, 2025
-
7 7 Skills Practice Scale Drawings And Models
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Domain Of The Relation Graphed Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
