What Is The Value Of X 105o 115o 125o 135o
Onlines
May 10, 2025 · 5 min read
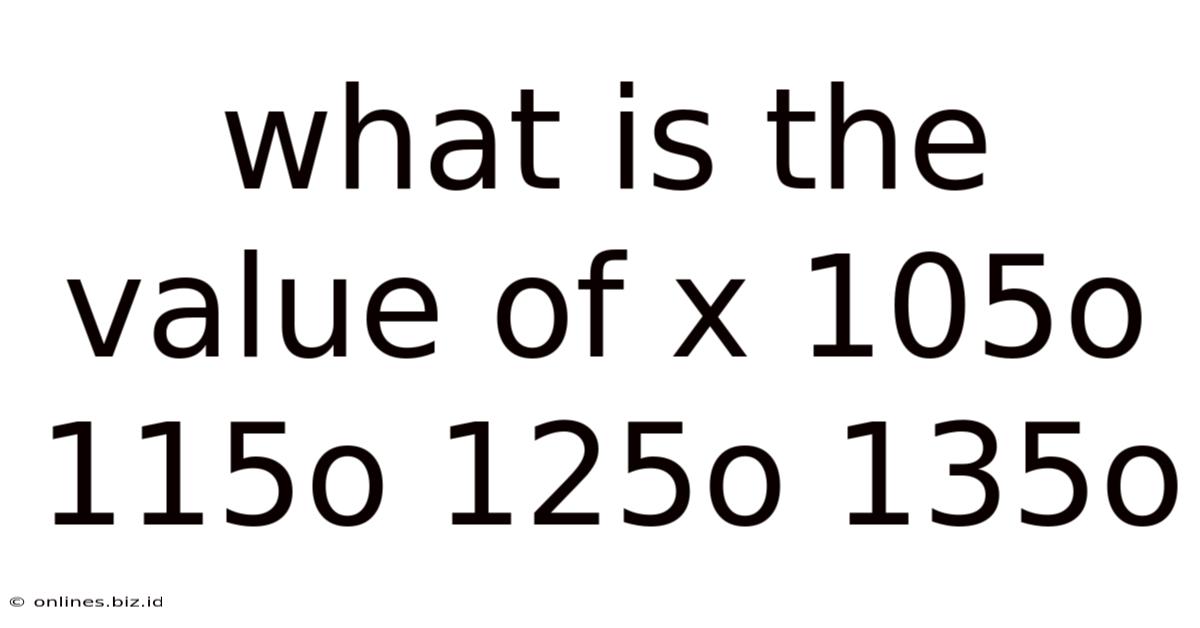
Table of Contents
What is the Value of x: Deciphering Angles and Their Relationships
This article delves into the fascinating world of geometry, specifically focusing on solving for an unknown angle, 'x', within a given set of angles: 105°, 115°, 125°, and 135°. We'll explore various approaches to determine the value of x, considering different geometric contexts and relationships between these angles. The process involves understanding fundamental concepts like supplementary angles, complementary angles, vertically opposite angles, angles on a straight line, and angles in polygons. We’ll also touch upon practical applications of these concepts.
Understanding Fundamental Angle Relationships
Before tackling the problem of finding 'x', it's crucial to review some key geometric principles:
1. Supplementary Angles:
Two angles are supplementary if their sum is 180°. For example, if angle A and angle B are supplementary, then A + B = 180°. This concept is frequently applied when angles are adjacent and form a straight line.
2. Complementary Angles:
Two angles are complementary if their sum is 90°. If angle C and angle D are complementary, then C + D = 90°. This is often seen in right-angled triangles.
3. Vertically Opposite Angles:
When two lines intersect, they form four angles. Vertically opposite angles are the angles directly opposite each other. These angles are always equal.
4. Angles on a Straight Line:
The angles on a straight line always add up to 180°. This is a direct application of the supplementary angles concept.
5. Angles in Polygons:
The sum of the interior angles of a polygon with 'n' sides is given by the formula (n-2) x 180°. For example, the sum of angles in a triangle (n=3) is (3-2) x 180° = 180°, and in a quadrilateral (n=4) it's (4-2) x 180° = 360°.
Possible Scenarios and Solutions for 'x'
The value of 'x' cannot be definitively determined without additional context. The angles 105°, 115°, 125°, and 135° could be related in many ways. Let's explore several possibilities:
Scenario 1: Angles in a Quadrilateral
If the angles 105°, 115°, 125°, and 135° are interior angles of a quadrilateral, their sum must be 360°. Let's check:
105° + 115° + 125° + 135° = 480°
Since the sum is 480°, these angles cannot form a quadrilateral. Therefore, in this context, 'x' cannot be found using this approach. Additional information would be necessary.
Scenario 2: Angles around a Point
If these angles are arranged around a single point, their sum should be 360°. Again, the sum is 480°, ruling out this possibility.
Scenario 3: Angles on a Straight Line and Vertically Opposite Angles
Let's consider various combinations. For example:
- Possibility A: Two pairs of supplementary angles. If 105° and x are supplementary, x = 180° - 105° = 75°. Similarly, other pairs could yield different values for x.
- Possibility B: Using vertically opposite angles. If 105° and x are vertically opposite, then x = 105°. The same logic can be applied to other angle pairs.
However, without a diagram or a clear description of how these angles are related, multiple values for 'x' are possible depending on the arrangement.
Scenario 4: Angles in a Polygon (Beyond Quadrilateral)
The angles could potentially be part of a polygon with more than four sides. However, finding the exact value of 'x' would require knowing the number of sides and the relationship of these angles within that polygon. The sum of the interior angles would be (n-2) * 180°, where 'n' is the number of sides. This would give us an equation involving 'x' and 'n', but without more information, it remains unsolvable.
The Importance of Context and Visual Representation
This exercise highlights the importance of providing sufficient context when dealing with geometric problems. The value of x is indeterminate based solely on the provided angles. A clear diagram illustrating the spatial arrangement of these angles is absolutely essential to determine the relationship between them and solve for x.
Practical Applications of Angle Relationships
Understanding angle relationships isn't just an academic pursuit; it has numerous practical applications:
-
Architecture and Construction: Architects and engineers rely heavily on geometry to ensure structural integrity and design aesthetically pleasing buildings. Accurate angle calculations are crucial for everything from roof construction to window placement.
-
Surveying and Mapping: Land surveyors use angle measurements to determine distances and create accurate maps of land parcels. This involves applying concepts of angles in triangles and other polygons.
-
Navigation: Pilots and sailors use angles to determine their position and navigate effectively. This involves understanding bearing angles and triangulation.
-
Computer Graphics and Game Development: Creating realistic 3D models and animations involves intricate calculations involving angles and rotations.
-
Robotics: Robotics relies on precise angle calculations to control the movement and positioning of robotic arms and other components.
Conclusion: The Power of Visual Information in Geometry
Determining the value of 'x' in this problem underscores the critical importance of visual information in geometry. While knowing the values of several angles is useful, it’s impossible to solve for 'x' without understanding their spatial arrangement. A clear diagram showing the relationships between the given angles would immediately unlock the solution.
This exercise serves as a valuable reminder of the fundamental principles of geometry and the need for clear and complete problem statements to arrive at accurate solutions. The problem highlights the importance of thorough understanding of supplementary angles, complementary angles, and angles in polygons, all of which are indispensable tools in various fields beyond mathematics. It also stresses the critical role of visualizing geometrical problems to unlock their solution. Always remember to draw diagrams – they are often the key to successfully solving geometric problems.
Latest Posts
Latest Posts
-
Lithium Metal Reacts With Liquid Bromine
May 11, 2025
-
Joaquim Wants To Create A Strong Professional
May 11, 2025
-
Alfred Lord Tennyson Ulysses Poem Summary
May 11, 2025
-
When A Cardholder Reports Their Gpc As Misplaced
May 11, 2025
-
Which Of The Following Statements About Tectonic Plates Is True
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 105o 115o 125o 135o . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.