Which Of The Following Functions Best Describes This Graph
Onlines
Apr 06, 2025 · 6 min read
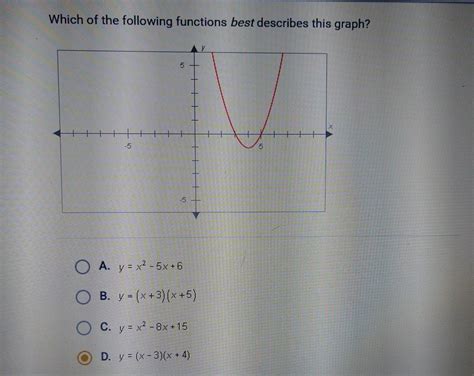
Table of Contents
Which of the Following Functions Best Describes This Graph? A Deep Dive into Function Identification
Identifying the function that best represents a given graph is a crucial skill in mathematics and data analysis. This ability allows us to model real-world phenomena, make predictions, and understand the underlying relationships within data sets. This article explores various function types – linear, quadratic, exponential, logarithmic, and sinusoidal – and provides a comprehensive methodology for determining which function best fits a specific graph. We'll delve into visual cues, analytical techniques, and practical examples to equip you with the tools needed to confidently analyze graphical data.
Understanding Different Function Types
Before we dive into graph analysis, let's refresh our understanding of the key function types commonly encountered:
1. Linear Functions: These functions represent a constant rate of change. Their graphs are straight lines. The general form is y = mx + c, where 'm' is the slope (rate of change) and 'c' is the y-intercept (the point where the line crosses the y-axis). Key visual cue: A straight line.
2. Quadratic Functions: These functions represent a changing rate of change. Their graphs are parabolas (U-shaped curves). The general form is y = ax² + bx + c, where 'a', 'b', and 'c' are constants. The value of 'a' determines the parabola's orientation (opens upwards if a > 0, downwards if a < 0). Key visual cue: A U-shaped curve.
3. Exponential Functions: These functions represent growth or decay that increases or decreases at an increasing rate. The general form is y = abˣ, where 'a' is the initial value and 'b' is the base (growth factor if b > 1, decay factor if 0 < b < 1). Key visual cue: A curve that increases or decreases rapidly, often approaching a horizontal asymptote.
4. Logarithmic Functions: These functions are the inverse of exponential functions. They represent growth or decay that slows down over time. The general form is y = logₐ(x), where 'a' is the base. Key visual cue: A curve that increases or decreases slowly, often approaching a vertical asymptote.
5. Sinusoidal Functions: These functions represent periodic oscillations, like waves. The general form is y = A sin(Bx + C) + D or y = A cos(Bx + C) + D, where A is the amplitude, B affects the period, C is the phase shift, and D is the vertical shift. Key visual cue: A repeating wave pattern.
A Step-by-Step Guide to Function Identification from a Graph
To determine which function best describes a graph, follow these steps:
Step 1: Analyze the Overall Shape:
- Is it a straight line? If yes, it's likely a linear function.
- Is it a U-shaped curve? If yes, it's likely a quadratic function.
- Does it increase or decrease rapidly, approaching a horizontal asymptote? If yes, it's likely an exponential function.
- Does it increase or decrease slowly, approaching a vertical asymptote? If yes, it's likely a logarithmic function.
- Does it show a repeating wave pattern? If yes, it's likely a sinusoidal function.
Step 2: Examine Key Features:
-
Intercepts: Note where the graph intersects the x-axis (x-intercepts or roots) and the y-axis (y-intercept). These points provide valuable information about the function. For example, the y-intercept of a linear function is 'c', and the x-intercepts of a quadratic function can help determine its factors.
-
Turning Points: For quadratic functions, identify the vertex (the minimum or maximum point). For sinusoidal functions, identify the maximum and minimum points and the period (the horizontal distance between two consecutive peaks or troughs).
-
Asymptotes: Identify any horizontal or vertical asymptotes. Exponential and logarithmic functions often exhibit asymptotes.
-
Symmetry: Observe if the graph is symmetric about the y-axis (even function) or the origin (odd function). This can help narrow down the possibilities.
Step 3: Consider the Context:
If the graph represents real-world data, consider the context. For instance, population growth often follows an exponential pattern, while the trajectory of a projectile might be represented by a quadratic function. Understanding the context can provide additional clues.
Step 4: Use Regression Analysis (for data points):
If you have a set of data points plotted on the graph, you can use regression analysis (linear regression, quadratic regression, exponential regression, etc.) to find the function that best fits the data. Many statistical software packages and calculators can perform regression analysis.
Examples: Identifying Functions from Graphs
Let's illustrate the process with some examples:
Example 1: A Straight Line
Imagine a graph showing a straight line passing through points (0, 2) and (1, 5). The slope (m) is (5-2)/(1-0) = 3, and the y-intercept (c) is 2. Therefore, the function is y = 3x + 2 (a linear function).
Example 2: A Parabola
Consider a parabola opening upwards with a vertex at (1, -2). This suggests a quadratic function of the form y = a(x-1)² - 2. If you know another point on the parabola, you can solve for 'a' and determine the exact function.
Example 3: Exponential Growth
A graph showing a curve that rapidly increases and approaches a horizontal asymptote at y = 0 suggests an exponential function of the form y = abˣ, where b > 1. The value of 'a' represents the initial value, and 'b' represents the growth factor.
Example 4: Logarithmic Decay
A graph exhibiting a curve that slowly decreases and approaches a vertical asymptote at x = 0 suggests a logarithmic function of the form y = logₐ(x), where the base 'a' is greater than 1 and the function is reflected across the x-axis to show decay.
Example 5: A Sinusoidal Wave
A graph showing a repeating wave pattern represents a sinusoidal function. By determining the amplitude, period, phase shift, and vertical shift from the graph, you can determine the specific equation (sine or cosine).
Advanced Techniques and Considerations
-
Transformations: Understanding function transformations (shifts, stretches, reflections) is crucial for identifying functions accurately. A shifted or scaled version of a basic function will still belong to the same function family.
-
Piecewise Functions: Some graphs might be represented by piecewise functions, where different functions are used for different parts of the domain.
-
Data Noise: Real-world data often contains noise (random fluctuations). When analyzing such data, focus on the overall trend rather than getting caught up in minor variations.
Conclusion
Identifying the function that best describes a given graph is a multifaceted skill that combines visual analysis, mathematical knowledge, and potentially, statistical techniques. By carefully examining the graph's shape, key features, and context, you can effectively determine the appropriate function type and, in many cases, even derive its precise equation. Mastering this skill empowers you to model and interpret data more effectively, leading to a deeper understanding of the underlying relationships and patterns. Remember to practice regularly with diverse graph examples to refine your ability to identify function types accurately and efficiently. This is a fundamental skill applicable across various scientific, engineering, and data-driven fields.
Latest Posts
Latest Posts
-
2 5b Exponential Function Context And Data Modeling
Apr 07, 2025
-
Amoeba Sisters Video Recap Introduction To Cells Answer Key
Apr 07, 2025
-
Which Of The Following Strategies Would Effectively Reduce Racism
Apr 07, 2025
-
The Open Boat Short Story Summary
Apr 07, 2025
-
Hartmans Nursing Assistant Care Workbook Answers Chapter 2
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Functions Best Describes This Graph . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.