Which Statement Correctly Compares The Centers Of The Distributions
Onlines
Apr 02, 2025 · 5 min read
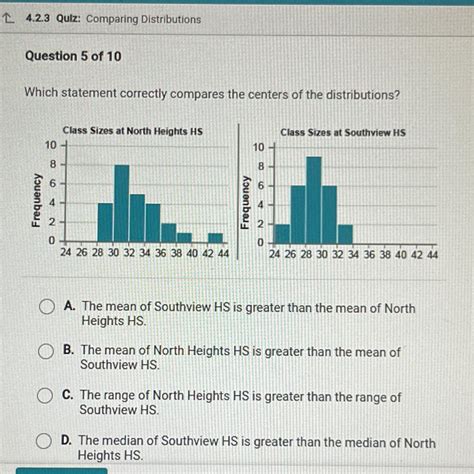
Table of Contents
Which Statement Correctly Compares the Centers of the Distributions? A Deep Dive into Statistical Analysis
Understanding how to compare the centers of different data distributions is a fundamental skill in statistics. Whether you're analyzing sales figures, student test scores, or biological measurements, accurately describing the central tendency of your data is crucial for drawing meaningful conclusions. This article provides a comprehensive guide to comparing distribution centers, covering various methods and scenarios, and offering practical examples to solidify your understanding.
What are the Centers of Distributions?
Before we delve into comparing centers, let's define what we mean. The "center" of a distribution refers to a single value that attempts to represent the typical or average value within the dataset. Several measures exist, each with its strengths and weaknesses:
- Mean: The average value, calculated by summing all values and dividing by the number of values. Highly sensitive to outliers (extreme values).
- Median: The middle value when the data is ordered. Less sensitive to outliers than the mean.
- Mode: The most frequent value. Useful for categorical data or data with multiple peaks.
The choice of which measure to use depends heavily on the nature of your data and the research question. A skewed distribution, for instance, might benefit from using the median rather than the mean as the center, as the mean can be significantly pulled in the direction of the skew.
Comparing Distributions: A Visual Approach
Before employing calculations, a visual inspection of the data is often the best starting point. Histograms, box plots, and dot plots provide excellent visual representations of the data's distribution, making it easier to qualitatively compare the centers.
- Histograms: Show the frequency of data values within specified intervals. Comparing the peaks of two histograms gives a quick, albeit rough, estimate of the difference in centers.
- Box Plots: Display the median, quartiles, and potential outliers. A direct visual comparison of the median lines in two box plots offers a clear indication of the difference in central tendency.
- Dot Plots: Show each data point individually. Useful for smaller datasets, they allow for easy visual identification of the clustering of data and a comparison of the central tendencies.
Comparing Distributions: Numerical Approaches
While visual methods provide a quick overview, numerical measures are needed for precise comparisons and statistical testing. The following methods are commonly used:
1. Comparing Means:
When comparing the means of two or more distributions, the difference between the means provides a direct comparison of their central tendencies. However, the significance of this difference needs to be assessed statistically, usually through hypothesis testing (t-test for independent samples, ANOVA for more than two groups) to determine if the difference is statistically significant or just due to random chance.
Example: Let's say you're comparing the average test scores of two classes. Class A has a mean score of 75, and Class B has a mean score of 82. The difference is 7 points, suggesting Class B performed better on average. However, a t-test would be required to determine if this difference is statistically significant considering the variability within each class's scores.
2. Comparing Medians:
For skewed distributions or datasets with outliers, comparing medians is a more robust approach. While there isn't a direct equivalent of a t-test for medians, non-parametric tests like the Mann-Whitney U test (for two independent samples) or the Kruskal-Wallis test (for more than two groups) can be used to compare the medians and assess the statistical significance of the difference.
3. Confidence Intervals:
Confidence intervals provide a range of values within which the true population mean (or median) is likely to fall with a certain level of confidence (e.g., 95%). If the confidence intervals of two distributions do not overlap, it suggests a statistically significant difference in their centers.
4. Effect Size:
Effect size measures quantify the magnitude of the difference between the centers of two distributions, irrespective of sample size. Common effect size measures for comparing means include Cohen's d and Hedge's g. These measures help determine the practical significance of the difference, providing context beyond just statistical significance.
Choosing the Right Method:
The choice of method depends on several factors:
- Data type: The mean is appropriate for numerical data, while the mode is suitable for categorical data. The median is robust to outliers and works well for both numerical and ordinal data.
- Data distribution: For normally distributed data, comparing means is appropriate. For skewed data, comparing medians is often preferred.
- Sample size: For small sample sizes, non-parametric tests are generally more robust.
- Research question: The specific research question will guide the choice of statistical test and effect size measure.
Common Mistakes in Comparing Distributions:
- Ignoring the data distribution: Assuming normality when the data is skewed can lead to inaccurate conclusions.
- Misinterpreting statistical significance: A statistically significant difference doesn't necessarily imply practical significance. The effect size should always be considered.
- Failing to account for outliers: Outliers can heavily influence the mean, leading to misleading comparisons.
- Using inappropriate statistical tests: Applying the wrong test can result in incorrect conclusions.
Advanced Considerations:
- Multiple comparisons: When comparing several distributions simultaneously, adjustments need to be made to account for multiple comparisons to avoid inflating the type I error rate (incorrectly rejecting the null hypothesis). Methods like Bonferroni correction can be applied.
- Non-parametric methods: When data violates the assumptions of parametric tests (like normality), non-parametric methods offer robust alternatives.
- Bayesian methods: Bayesian approaches provide a different framework for comparing distributions, allowing the incorporation of prior knowledge and providing posterior distributions that reflect the uncertainty in the estimates.
Conclusion:
Comparing the centers of distributions is a fundamental task in statistical analysis. Choosing the appropriate method – whether visual or numerical – depends on the nature of your data, your research question, and the assumptions you can make about your data. Always consider the data distribution, potential outliers, and the practical significance of any observed differences. By carefully selecting and interpreting the appropriate statistical techniques, you can draw accurate and meaningful conclusions about the differences in central tendency between your datasets. Remember to always pair your numerical analysis with a visual representation of the data to gain a holistic understanding of the distributions you are comparing. This comprehensive approach will help you confidently address questions about which statement correctly compares the centers of the distributions you're analyzing.
Latest Posts
Latest Posts
-
Medical Terminology Crossword Puzzle Answer Key
Apr 03, 2025
-
The Paper Is Stating The Poems Summaries Themes Topics Transitions
Apr 03, 2025
-
Hw 7 1 1 3 Arithmetic And Geometric Sequences
Apr 03, 2025
-
A Client With Copd Has A Blood Ph Of 7 25
Apr 03, 2025
-
What Is The Best Way To Prevent Ratio Strain
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Which Statement Correctly Compares The Centers Of The Distributions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
