2 4 Practice Writing Linear Equations
Onlines
Apr 01, 2025 · 5 min read
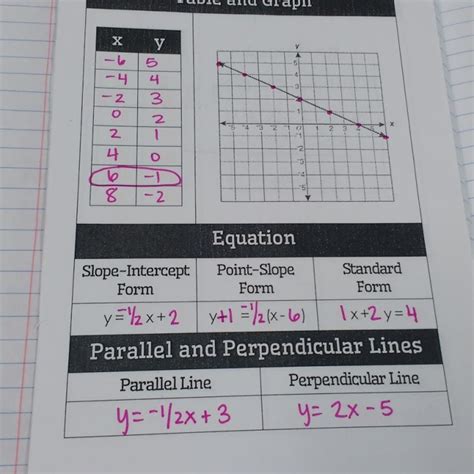
Table of Contents
24 Practice Writing Linear Equations: Mastering the Fundamentals
Linear equations form the bedrock of algebra, and a solid understanding is crucial for success in higher-level mathematics. This comprehensive guide provides 24 practice problems covering various aspects of writing linear equations, progressing from simpler to more complex scenarios. We'll explore different forms of linear equations, including slope-intercept, point-slope, and standard form, and delve into strategies for tackling word problems. Whether you're a student aiming to ace your next algebra test or simply looking to refresh your math skills, this guide will help you master the art of writing linear equations.
Understanding the Basics: Forms of Linear Equations
Before diving into the practice problems, let's quickly recap the three primary forms of linear equations:
1. Slope-Intercept Form: y = mx + b
- m represents the slope (the steepness of the line). A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend.
- b represents the y-intercept (the point where the line crosses the y-axis).
This form is ideal when you know the slope and y-intercept.
2. Point-Slope Form: y - y₁ = m(x - x₁)
- m represents the slope.
- (x₁, y₁) represents a point on the line.
This form is useful when you know the slope and a point on the line.
3. Standard Form: Ax + By = C
- A, B, and C are integers (whole numbers).
- A is typically non-negative.
This form is often used for general representation and is particularly helpful in certain applications.
24 Practice Problems: Writing Linear Equations
Now, let's get to the heart of the matter – practice problems! Remember to show your work step-by-step to fully grasp the concepts.
Section 1: Using Slope and Intercept
- Write the equation of a line with a slope of 2 and a y-intercept of 5.
- Write the equation of a line with a slope of -3 and a y-intercept of -1.
- A line has a slope of 1/2 and passes through the point (0, 3). Write its equation.
- Find the equation of a line with a slope of 0 and a y-intercept of 7.
- A horizontal line passes through the point (4, -2). Write its equation.
Section 2: Using Slope and a Point
- Write the equation of a line with a slope of 4 that passes through the point (1, 2).
- Find the equation of a line with a slope of -1/3 that passes through the point (-3, 1).
- A line passes through the points (2, 5) and (4, 9). Find its equation. (Hint: First find the slope).
- A line passes through the points (-1, -2) and (3, 2). Find its equation.
- A line has a slope of 2 and passes through the point (0,0). Write its equation.
Section 3: Using Two Points
- Write the equation of the line passing through (1, 3) and (2, 5).
- Find the equation of the line passing through (-2, 4) and (0, 0).
- A line passes through (3, -1) and (-3, 5). Write its equation in slope-intercept form.
- Determine the equation of the line passing through (0, 2) and (4, 6).
- Find the equation of the line passing through (-1, 1) and (1, -1).
Section 4: Word Problems
- A taxi charges a $3 initial fee plus $2 per mile. Write an equation to represent the total cost (y) as a function of miles driven (x).
- A plant grows 2 inches per week. It starts at a height of 4 inches. Write an equation to represent its height (y) after x weeks.
- The temperature starts at 10 degrees Celsius and increases by 3 degrees per hour. Write an equation representing the temperature (y) after x hours.
- A phone plan charges a monthly fee of $25 plus $0.10 per minute. Write an equation representing the total monthly cost (y) based on minutes used (x).
- A car depreciates in value by $2000 per year. If it's initially worth $20,000, write an equation to represent its value (y) after x years.
Section 5: Converting Between Forms
- Convert the equation 2x + y = 6 into slope-intercept form.
- Convert the equation y - 3 = 2(x - 1) into standard form.
- Convert the equation y = -x + 4 into standard form.
- Convert the equation x = 5 into standard form.
Solutions and Further Practice
This section will not provide the solutions directly but will offer hints and guiding principles for each problem. Solving these problems yourself is key to mastering the concept. Remember to consult your textbook or online resources if you get stuck.
Hints for Solving:
- Remember your slope formula: (y₂ - y₁) / (x₂ - x₁)
- Substitute carefully: Double-check your substitutions in each equation.
- Simplify: Always simplify your equations to their simplest form.
- Check your work: Plug in a point from the problem into your final equation to ensure it satisfies the equation.
For further practice, you can create your own problems using different points and slopes, or search online for more practice exercises. You could also try to create real-world scenarios that require you to write linear equations. The more you practice, the more confident you will become in writing linear equations. Remember, understanding the relationships between the different forms of linear equations is crucial.
Mastering Linear Equations: Beyond the Basics
Writing linear equations is a fundamental skill that builds a strong foundation for more advanced algebraic concepts. By diligently working through these practice problems and consistently reviewing the different forms of linear equations, you will not only improve your problem-solving skills but also gain a deeper appreciation for the power and versatility of linear equations. This foundation is essential for understanding graphs, systems of equations, and various applications in fields such as physics, engineering, and economics. Continuous practice and a methodical approach are your keys to success! Remember to focus on understanding the underlying concepts rather than just memorizing formulas. This approach will allow you to tackle more complex problems and applications confidently. Good luck, and happy equation-solving!
Latest Posts
Latest Posts
-
Which Is An Identifying Characteristic Of Acrylic Plastics
Apr 02, 2025
-
Match Each Description With The Appropriate Step In Enzyme Catalysis
Apr 02, 2025
-
Unit 7 Right Triangles And Trigonometry Homework 4 Answers Key
Apr 02, 2025
-
Ap English Language And Composition Section 1 Answer Key
Apr 02, 2025
-
Cloze Ing In On Science Organisms And Environments Answers
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 2 4 Practice Writing Linear Equations . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
