7-61 Draw The Shear And Moment Diagrams For The Beam
Onlines
Apr 05, 2025 · 7 min read
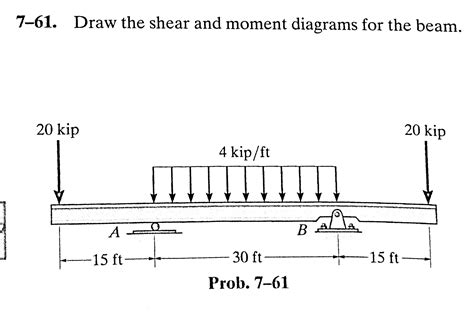
Table of Contents
7-61: Drawing Shear and Moment Diagrams for a Beam
Determining shear and moment diagrams is crucial in structural analysis. These diagrams visually represent the internal forces acting within a beam under various loading conditions, allowing engineers to assess stress levels and ensure structural integrity. This comprehensive guide will walk you through the process of constructing shear and moment diagrams for a beam described as "7-61," assuming a specific loading scenario (as the problem statement alone is insufficient for a complete solution). We'll cover various methods, including the direct integration method and the equilibrium method, emphasizing practical application and understanding.
Understanding Shear and Moment Diagrams
Before diving into the specific problem, let's clarify the fundamentals.
Shear Force
Shear force represents the internal force acting parallel to the cross-section of the beam. It's the algebraic sum of all vertical forces acting on either side of the considered section. A positive shear force typically indicates upward shear on the left side of a section. Understanding shear forces is critical for assessing shear stress, which can cause failure through shear fracturing.
Bending Moment
The bending moment is the internal resisting moment within the beam caused by external forces. It's the algebraic sum of the moments of all forces acting on either side of a section about that section. A positive bending moment typically creates sagging (curvature downwards). Bending moments are crucial for evaluating bending stress, responsible for bending failure.
Methods for Constructing Shear and Moment Diagrams
Several methods exist for creating these diagrams. We'll focus on two prevalent approaches:
1. The Equilibrium Method (Using Free Body Diagrams)
This method is highly intuitive and generally preferred for simpler beams with discrete loads. It relies on analyzing free body diagrams (FBDs) of segments of the beam.
Steps:
- Draw the complete free body diagram (FBD) of the beam: Include all external loads, reactions (calculated using equilibrium equations – ΣF<sub>x</sub> = 0, ΣF<sub>y</sub> = 0, ΣM = 0), and dimensions.
- Section the beam: Imagine cutting the beam at various points along its length.
- Draw FBDs for each section: Show the internal shear force (V) and bending moment (M) acting at the cut section. The directions of V and M are crucial and must be assumed; if the calculated value is negative, it means your initial assumption of direction was incorrect.
- Apply equilibrium equations: For each section, apply ΣF<sub>y</sub> = 0 to determine the shear force (V) and ΣM = 0 (taking moments about the cut section) to determine the bending moment (M).
- Plot the values: Plot the calculated shear forces (V) against the corresponding distances along the beam's length to create the shear diagram. Similarly, plot the bending moments (M) to generate the moment diagram.
2. The Direct Integration Method
This method is suitable for beams with distributed loads or complex loading scenarios. It involves integrating the load function to find the shear function and integrating the shear function to find the moment function.
Steps:
- Define the load function (w(x)): Express the distributed load as a function of the distance along the beam.
- Integrate the load function: Integrate w(x) with respect to x to obtain the shear function, V(x) = ∫w(x)dx + C<sub>1</sub>, where C<sub>1</sub> is the constant of integration determined from boundary conditions (shear at a known point).
- Integrate the shear function: Integrate V(x) with respect to x to obtain the moment function, M(x) = ∫V(x)dx + C<sub>2</sub>, where C<sub>2</sub> is another constant of integration determined from boundary conditions (moment at a known point).
- Plot the functions: Plot V(x) and M(x) against x to obtain the shear and moment diagrams.
Example Application to a Hypothetical "7-61" Beam
Let's assume a specific loading condition for a beam labelled "7-61" to illustrate the methods. Remember that this is a hypothetical example; a real "7-61" beam would require a specific problem statement detailing the beam's dimensions and loading.
Hypothetical Scenario:
Consider a simply supported beam "7-61" of length L = 10 meters. It carries a uniformly distributed load (UDL) of w = 2 kN/m over its entire length and a point load of P = 5 kN at x = 3 meters from the left support.
Solution using the Equilibrium Method:
-
Calculate Reactions: Using equilibrium equations (ΣF<sub>y</sub> = 0 and ΣM = 0), determine the reactions at the supports.
- R<sub>A</sub> + R<sub>B</sub> = 20 kN + 5 kN = 25 kN (ΣF<sub>y</sub> = 0)
- R<sub>B</sub> * 10 m = (2 kN/m * 10 m * 5 m) + (5 kN * 7 m) = 100 kN.m + 35 kN.m = 135 kN.m
- R<sub>B</sub> = 13.5 kN
- R<sub>A</sub> = 25 kN - 13.5 kN = 11.5 kN
-
Section the beam: Imagine cutting the beam at various points.
-
Analyze sections: We'll consider three sections:
- 0 < x < 3 m: V(x) = 11.5 kN - 2x kN; M(x) = 11.5x - x² kN.m
- 3 m < x < 10 m: V(x) = 11.5 kN - 2x kN + 5 kN = 16.5 kN - 2x kN; M(x) = 11.5x - x² + 5(x-3) kN.m = 16.5x - x² -15 kN.m
-
Plot the diagrams: Using the equations above, we can plot the shear and moment diagrams. The shear diagram will show a linearly decreasing shear force from 11.5 kN at x=0 to a value of 11.5 - 6 = 5.5 kN at x=3m, and then a further linear decrease to -13.5 kN at x=10m. The moment diagram will be a parabola with a maximum value somewhere between x=0 and x=10m.
Solution using the Direct Integration Method:
-
Load Function: w(x) = 2 kN/m + 5 kN * δ(x-3) (where δ represents the Dirac delta function for the point load).
-
Shear Function: V(x) = ∫w(x)dx + C<sub>1</sub> = 2x + 5H(x-3) + C<sub>1</sub> (where H represents the Heaviside step function). Using boundary condition V(0) = 11.5 kN, C<sub>1</sub> = 11.5 kN.
-
Moment Function: M(x) = ∫V(x)dx + C<sub>2</sub> = x² + 5(x-3)H(x-3) + 11.5x + C<sub>2</sub>. Using boundary condition M(0) = 0, C<sub>2</sub> = 0.
-
Plot the diagrams: Plotting the shear and moment functions derived from direct integration yields the same shear and moment diagrams as obtained using the equilibrium method. Note that careful handling of the step and delta functions is crucial in this method.
Interpreting the Diagrams
The shear and moment diagrams provide valuable information:
- Maximum Shear Force: Identifies the location and magnitude of the maximum shear stress, critical for assessing shear failure potential.
- Maximum Bending Moment: Indicates the location and magnitude of the maximum bending stress, crucial for determining bending failure risk.
- Points of Inflection: Where the moment diagram changes sign; these points are crucial in understanding the curvature change in the beam.
Advanced Considerations
This guide provides a fundamental understanding. For more complex beams (e.g., continuous beams, beams with overhanging ends, indeterminate beams) more sophisticated analysis techniques, including matrix methods, are needed. Software tools can significantly assist in analyzing these more complicated structures.
Remember to always verify your calculations and diagrams using different methods and consider the limitations of your assumptions. Precise drawing and clear labeling are also essential for accurate interpretation and effective communication. The analysis presented here assumes linear elastic material behavior and small deflections. For large deflections or non-linear materials, more advanced analysis techniques are required. This detailed explanation should help in creating accurate and comprehensive shear and moment diagrams for beam 7-61 (or any similar beam problem) and contribute towards a strong understanding of structural analysis principles.
Latest Posts
Latest Posts
-
Theme Of The Road Cormac Mccarthy
Apr 06, 2025
-
Ap Macroeconomics Unit 1 Test Answers
Apr 06, 2025
-
Which Of The Following Characterizes Critical Thinkers
Apr 06, 2025
-
University Of The People Academic Honesty Policy
Apr 06, 2025
-
10 4 Study Guide And Intervention Inscribed Angles Answer Key
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 7-61 Draw The Shear And Moment Diagrams For The Beam . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
