A Parallel Rlc Circuit Must Contain At Least Three Branches.
Onlines
Apr 05, 2025 · 6 min read
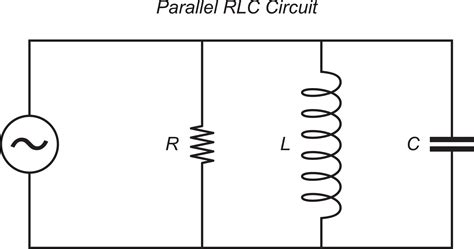
Table of Contents
A Parallel RLC Circuit Must Contain at Least Three Branches: A Deep Dive into Circuit Analysis
The statement "a parallel RLC circuit must contain at least three branches" is fundamental to understanding the behavior and analysis of this crucial circuit configuration. This article will delve into the reasons behind this assertion, exploring the characteristics of parallel RLC circuits, their applications, and the mathematical tools used to analyze their behavior. We'll also consider variations and edge cases to solidify the understanding of this core concept.
Understanding the Basic Structure of a Parallel RLC Circuit
A parallel RLC circuit, as its name suggests, consists of a resistor (R), an inductor (L), and a capacitor (C) connected in parallel across a voltage source or input signal. This configuration is distinct from the series RLC circuit where the components are connected end-to-end. The key feature highlighting the necessity of three branches is the parallel connection itself. Each component forms its own individual branch, resulting in at least three current paths from the voltage source.
- Branch 1: The resistive branch, containing only the resistor (R).
- Branch 2: The inductive branch, containing only the inductor (L).
- Branch 3: The capacitive branch, containing only the capacitor (C).
The presence of these three branches is not merely a structural detail; it's the foundation of the circuit's unique characteristics and behavior. Removing any one branch fundamentally alters the circuit's response, transforming it into a different type of circuit altogether (e.g., a parallel RC or RL circuit).
Why Three Branches are Essential
The necessity of three branches stems directly from the independent current paths created by the parallel configuration. Each component responds to the applied voltage differently, resulting in distinct branch currents:
-
Resistive Branch (I<sub>R</sub>): The current through the resistor is directly proportional to the applied voltage and is given by Ohm's law: I<sub>R</sub> = V/R. It's always in phase with the voltage.
-
Inductive Branch (I<sub>L</sub>): The current through the inductor lags the applied voltage by 90 degrees. It's determined by the voltage and the inductive reactance (X<sub>L</sub> = 2πfL, where f is the frequency). I<sub>L</sub> = V/X<sub>L</sub>.
-
Capacitive Branch (I<sub>C</sub>): The current through the capacitor leads the applied voltage by 90 degrees. It's determined by the voltage and the capacitive reactance (X<sub>C</sub> = 1/(2πfC)). I<sub>C</sub> = V/X<sub>C</sub>.
The total current (I<sub>T</sub>) drawn from the source is the sum of these three branch currents: I<sub>T</sub> = I<sub>R</sub> + I<sub>L</sub> + I<sub>C</sub>. This crucial relationship highlights the independent nature of each branch and demonstrates why three branches are needed to characterize a parallel RLC circuit.
Mathematical Analysis and Implications
Analyzing a parallel RLC circuit involves applying Kirchhoff's Current Law (KCL), which states that the sum of currents entering a node is equal to the sum of currents leaving that node. In our case, the node is the junction point where the three branches connect to the voltage source. Therefore, KCL gives us:
I<sub>T</sub> = I<sub>R</sub> + I<sub>L</sub> + I<sub>C</sub>
This equation, combined with the individual branch current equations mentioned earlier, allows us to completely analyze the circuit's behavior in both the time and frequency domains. This analysis often leads to the determination of the circuit's:
-
Resonant Frequency (f<sub>0</sub>): The frequency at which the inductive and capacitive reactances cancel each other out (X<sub>L</sub> = X<sub>C</sub>). At resonance, the total current is at its minimum (and impedance is maximum) in a parallel RLC circuit.
-
Bandwidth: A measure of the range of frequencies over which the circuit's response is significant.
-
Quality Factor (Q): A measure of the circuit's selectivity or sharpness of resonance. A higher Q factor indicates a narrower bandwidth and a sharper resonance.
These parameters are critical in designing and understanding the application of parallel RLC circuits.
Applications of Parallel RLC Circuits
Parallel RLC circuits find widespread application in various electrical and electronic systems due to their unique frequency response characteristics. Some prominent examples include:
-
Resonant Filters: They are extensively used in filter circuits to select or reject specific frequencies. By carefully choosing the component values (R, L, and C), engineers can design band-pass filters (allowing a specific range of frequencies to pass) or band-stop filters (rejecting a specific range of frequencies). These are crucial in signal processing, communication systems, and audio applications.
-
Tank Circuits: These circuits, which use a parallel combination of L and C, are used in oscillators to generate specific frequencies. They provide positive feedback necessary for oscillation.
-
Power Factor Correction: Parallel RLC circuits can be employed to improve the power factor in AC circuits, reducing energy losses and improving the efficiency of electrical systems. This is especially important in high-power applications.
-
Tuning Circuits: In radio receivers and other tuning applications, a parallel LC circuit (essentially a parallel RLC circuit with a very high R value representing the coil resistance) is used to select a specific radio frequency from a range of frequencies.
These applications highlight the importance of understanding the fundamental three-branch structure and its impact on the circuit's overall functionality.
Variations and Edge Cases
While the basic parallel RLC circuit comprises three distinct branches, there are variations and edge cases to consider.
-
Ideal Case vs. Real-world Components: In theoretical analysis, we often assume ideal components (no resistance in inductors or capacitors). However, real-world components have parasitic resistances and capacitances, impacting the circuit's performance. These parasitic elements effectively modify the value of R, adding some complexity to the analysis, but it doesn't change the need for at least three fundamental branches.
-
Multiple Components in a Branch: While the fundamental definition necessitates three branches, it's possible to have multiple resistors, inductors, or capacitors within a single branch. The equivalent impedance of such a branch would be used in circuit analysis. This simplification, however, doesn't negate the need for at least three separate branches in the basic framework.
-
RL or RC Circuits as Subsets: It’s possible to imagine scenarios where one of the components is absent (e.g., L is removed). In such cases, the circuit would then become a parallel RC or RL circuit. These are subsets of the broader parallel RLC classification and are simpler due to the fewer current paths. They aren't considered parallel RLC circuits because the presence of all three elements is the defining factor.
Conclusion
A parallel RLC circuit inherently requires at least three branches—one for each component (R, L, and C)—because each component provides an independent current path in the parallel configuration. This three-branch structure directly influences the circuit's unique frequency response, enabling a wide array of applications in resonant filters, tank circuits, and power factor correction. Mathematical analysis using KCL and the consideration of component characteristics (including real-world considerations) fully define the circuit's behavior and performance. Understanding this fundamental characteristic is essential for anyone working with electrical circuits and their design. Failing to recognize the three-branch structure would result in an incorrect model and therefore inaccurate analysis and design.
Latest Posts
Latest Posts
-
The Lesson Summary Toni Cade Bambara
Apr 05, 2025
-
Chapter 1 Summary Of Catcher In The Rye
Apr 05, 2025
-
Find The Probability That X Falls In The Shaded Area
Apr 05, 2025
-
The Patriot Movie Questions And Answers
Apr 05, 2025
-
Secondary Math 1 Module 5 3 Answer Key
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about A Parallel Rlc Circuit Must Contain At Least Three Branches. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
