Here Is A Graph Of The Function H
Onlines
Mar 26, 2025 · 6 min read
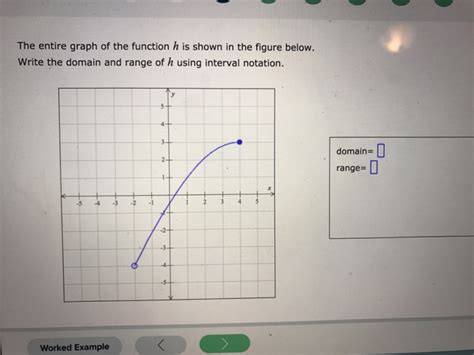
Table of Contents
Decoding the Graph: A Comprehensive Analysis of Function h
This article delves deep into the analysis of a function represented graphically, denoted as 'h'. We will explore various aspects, including domain and range, identifying key features like intercepts, asymptotes, extrema (maxima and minima), intervals of increase and decrease, concavity, and inflection points. Furthermore, we'll discuss how to potentially derive the algebraic representation of 'h' from its graphical representation, focusing on common function types. This comprehensive analysis will equip you with the skills to interpret and understand the behavior of functions presented graphically.
Understanding the Fundamentals: What a Graph Tells Us
Before we dive into the specifics, it's crucial to understand what information a graph of a function provides. A graph visually represents the relationship between the input values (x-values, or the domain) and the corresponding output values (y-values, or the range) of a function. Each point (x, y) on the graph indicates that when the input is 'x', the output is 'y'.
Analyzing the graph allows us to:
-
Determine the Domain and Range: The domain encompasses all possible input values (x-values) for which the function is defined. The range represents all possible output values (y-values) the function can produce. Visually, the domain is the span of the graph along the x-axis, and the range is the span along the y-axis.
-
Identify Intercepts: The x-intercepts are the points where the graph intersects the x-axis (y=0). These points represent the roots or zeros of the function. The y-intercept is the point where the graph intersects the y-axis (x=0). This point represents the function's value when the input is zero.
-
Locate Asymptotes: Asymptotes are lines that the graph approaches but never touches. Vertical asymptotes occur when the function's value approaches positive or negative infinity at a specific x-value. Horizontal asymptotes represent the behavior of the function as x approaches positive or negative infinity.
-
Find Extrema (Maxima and Minima): Extrema are the maximum or minimum values of the function within a specific interval or the entire domain. Local maxima are peaks, while local minima are troughs on the graph. Global maxima and minima represent the absolute highest and lowest points on the graph, respectively.
-
Analyze Intervals of Increase and Decrease: A function is increasing over an interval if its y-values increase as the x-values increase. Conversely, it's decreasing if its y-values decrease as the x-values increase.
-
Determine Concavity and Inflection Points: Concavity refers to the curvature of the graph. A graph is concave up if it curves upward, resembling a "U" shape, and concave down if it curves downward, resembling an inverted "U" shape. Inflection points are points where the concavity changes from upward to downward or vice-versa.
Analyzing a Sample Graph (Hypothetical)
Let's assume our graph of function 'h' exhibits the following characteristics (note: this is a hypothetical example; you would replace this with your actual graph):
- Domain: (-∞, 2) ∪ (2, ∞) (This suggests a vertical asymptote at x = 2)
- Range: (-∞, 4)
- x-intercept: Approximately x = 1
- y-intercept: Approximately y = 3
- Vertical Asymptote: x = 2
- Horizontal Asymptote: y = 0
- Local Maximum: Approximately at (0, 4)
- Increasing Interval: (-∞, 0)
- Decreasing Interval: (0, 2) and (2, ∞)
- Concave Up: (2, ∞)
- Concave Down: (-∞, 2)
- No Inflection Points: In this case
Deriving a Possible Algebraic Representation
Based on the characteristics above, we can try to deduce a possible algebraic expression for the function 'h'. Given the vertical asymptote at x=2 and the horizontal asymptote at y=0, a rational function is a likely candidate. A rational function is a function that can be expressed as the quotient of two polynomial functions.
A plausible (but not necessarily unique) form for 'h(x)' might be:
h(x) = A / (x - 2) + B
Where 'A' and 'B' are constants. We can estimate 'A' and 'B' using the information from the graph. For example, the y-intercept (approximately 3) could be used:
3 = A / (0 - 2) + B
We also need to consider the local maximum at (0, 4). This will further constrain the values of A and B. However, finding precise values of A and B would require more precise information from the graph. This process can be complex, requiring techniques like curve fitting and potentially employing software tools designed for such analysis.
Advanced Analysis Techniques
For more complex graphs, sophisticated techniques may be necessary:
-
Calculus: Using calculus, specifically derivatives, is essential for precisely determining intervals of increase/decrease, concavity, and inflection points. The first derivative, h'(x), helps identify critical points (where the slope is zero or undefined), indicating potential maxima and minima. The second derivative, h''(x), reveals concavity. Points where h''(x) changes sign are inflection points.
-
Numerical Methods: If an explicit algebraic expression is difficult or impossible to derive, numerical methods can be used to approximate the function's behavior at different points. This might involve using interpolation or regression techniques.
-
Software Tools: Mathematical software packages (like MATLAB, Mathematica, or even online graphing calculators) can assist in analyzing graphs, fitting curves, and providing numerical approximations. These tools offer capabilities for symbolic computation and numerical analysis, aiding in more precise estimations of function parameters.
Practical Applications
Understanding and analyzing graphs of functions isn't just a theoretical exercise; it has wide-ranging applications across numerous fields:
-
Engineering: In fields like mechanical or electrical engineering, graphs represent system behavior. Analyzing these graphs is crucial for predicting system performance, stability, and identifying potential issues.
-
Economics: Demand curves, supply curves, and cost functions are represented graphically. Analyzing these graphs allows economists to understand market dynamics, make predictions, and design economic policies.
-
Science: Scientific data is frequently presented graphically. Analyzing these graphs helps scientists identify trends, relationships, and draw conclusions about the phenomena under study.
-
Data Science: Data visualization is a cornerstone of data analysis. Understanding how to interpret graphs is essential for extracting meaningful insights from datasets.
Conclusion: A Holistic Approach to Graph Analysis
Analyzing a graph of a function, whether simple or complex, requires a methodical approach. Begin by visually inspecting the graph to identify key features like intercepts, asymptotes, and extrema. Then, apply theoretical knowledge of functions and, if necessary, calculus techniques to rigorously determine intervals of increase/decrease, concavity, and inflection points. In cases where an explicit algebraic expression is needed, consider applying curve fitting or employing numerical methods and software tools to derive a suitable representation. Mastering this process will greatly enhance your ability to understand and interpret the behavior of functions and apply this knowledge to various real-world applications. Remember, practice makes perfect! The more graphs you analyze, the sharper your skills will become.
Latest Posts
Latest Posts
-
Summary Of The Crucible Act 3
Mar 29, 2025
-
As An Emt The Performance Of Your Duties
Mar 29, 2025
-
The Pinning Ceremony Signifies Which Of The Following
Mar 29, 2025
-
Ap Csa Unit 9 Progress Check Frq
Mar 29, 2025
-
Nurses Who Value Client Advocacy Follow What Guideline
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Here Is A Graph Of The Function H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
