Homework 4 Trigonometric Ratios & Finding Missing Sides
Onlines
Mar 26, 2025 · 6 min read
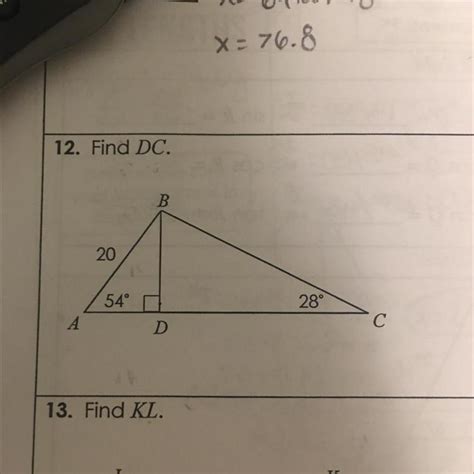
Table of Contents
Homework 4: Trigonometric Ratios & Finding Missing Sides
Trigonometry, derived from the Greek words "trigonon" (triangle) and "metron" (measure), is the branch of mathematics that deals with the relationships between angles and sides of triangles. This foundational concept underpins numerous applications in various fields, from architecture and engineering to physics and computer graphics. This article delves into trigonometric ratios – sine, cosine, and tangent – and their application in determining the lengths of missing sides in right-angled triangles.
Understanding Trigonometric Ratios
The heart of trigonometry lies in the three primary ratios: sine (sin), cosine (cos), and tangent (tan). These ratios relate the lengths of the sides of a right-angled triangle to its angles. Remember, a right-angled triangle is a triangle containing one 90-degree angle.
Let's consider a right-angled triangle with a right angle at C. We'll label the sides relative to angle A:
- Hypotenuse: The side opposite the right angle (side AB). This is always the longest side of the right-angled triangle.
- Opposite: The side opposite angle A (side BC).
- Adjacent: The side next to angle A (side AC).
Now, let's define the trigonometric ratios:
- Sine (sin A) = Opposite / Hypotenuse (BC / AB)
- Cosine (cos A) = Adjacent / Hypotenuse (AC / AB)
- Tangent (tan A) = Opposite / Adjacent (BC / AC)
It's crucial to remember that these ratios are specific to the angle you are considering (in this case, angle A). If you were working with angle B, the opposite and adjacent sides would switch places.
Applying Trigonometric Ratios to Find Missing Sides
The power of trigonometric ratios lies in their ability to solve for unknown sides in right-angled triangles when we know at least one angle (other than the right angle) and one side. Let's explore various scenarios:
Scenario 1: Finding the Opposite Side
Suppose you know the angle A and the length of the hypotenuse (AB). You want to find the length of the opposite side (BC). You would use the sine ratio:
sin A = Opposite / Hypotenuse
Rearranging the formula to solve for the opposite side:
Opposite = sin A * Hypotenuse
Example:
If angle A = 30° and the hypotenuse (AB) = 10 cm, then:
Opposite = sin 30° * 10 cm = 0.5 * 10 cm = 5 cm
Therefore, the length of the opposite side (BC) is 5 cm.
Scenario 2: Finding the Adjacent Side
If you know angle A and the length of the hypotenuse (AB), and you need to find the adjacent side (AC), you'll use the cosine ratio:
cos A = Adjacent / Hypotenuse
Solving for the adjacent side:
Adjacent = cos A * Hypotenuse
Example:
If angle A = 45° and the hypotenuse (AB) = 8 cm, then:
Adjacent = cos 45° * 8 cm ≈ 0.707 * 8 cm ≈ 5.66 cm
Therefore, the length of the adjacent side (AC) is approximately 5.66 cm.
Scenario 3: Finding the Opposite Side when knowing the Adjacent Side
You might encounter situations where you know angle A and the length of the adjacent side (AC), and you need to find the opposite side (BC). In this case, the tangent ratio comes into play:
tan A = Opposite / Adjacent
Solving for the opposite side:
Opposite = tan A * Adjacent
Example:
If angle A = 60° and the adjacent side (AC) = 4 cm, then:
Opposite = tan 60° * 4 cm ≈ 1.732 * 4 cm ≈ 6.93 cm
Therefore, the length of the opposite side (BC) is approximately 6.93 cm.
Scenario 4: Finding the Hypotenuse
Sometimes, you know an angle and one of the other sides, and you need to find the hypotenuse. You can use either the sine or cosine ratio, depending on which side you already know:
- If you know the opposite side: Use the sine ratio: Hypotenuse = Opposite / sin A
- If you know the adjacent side: Use the cosine ratio: Hypotenuse = Adjacent / cos A
Example (using sine):
If angle A = 25° and the opposite side (BC) = 7 cm, then:
Hypotenuse = 7 cm / sin 25° ≈ 7 cm / 0.423 ≈ 16.55 cm
Practical Applications and Real-World Examples
The applications of trigonometric ratios in finding missing sides extend far beyond textbook problems. Here are some real-world examples:
-
Surveying: Land surveyors use trigonometry to measure distances and heights indirectly. By measuring angles and a known distance, they can calculate the heights of buildings or the distances across rivers or inaccessible terrains.
-
Engineering: Engineers use trigonometry in designing structures like bridges and buildings. They need to calculate the forces acting on different parts of the structure, and trigonometric ratios are essential for determining the lengths of beams and other components.
-
Navigation: Pilots and sailors utilize trigonometry for navigation. They can determine their position by measuring angles to known landmarks and using trigonometric ratios to calculate distances.
-
Computer Graphics: Trigonometric functions are fundamental in computer graphics for creating realistic images and animations. They are used to model the movement of objects and to calculate the positions of objects on the screen.
-
Physics: Trigonometry plays a vital role in physics, particularly in areas like projectile motion and forces. Analyzing the trajectory of a projectile involves using trigonometric ratios to break down the velocity vector into its horizontal and vertical components.
Advanced Concepts and Further Exploration
While this article focuses on the basics of trigonometric ratios and their application to right-angled triangles, there's much more to explore in the world of trigonometry. Some advanced concepts include:
-
Trigonometric Identities: These are equations that are true for all values of the angles involved. Understanding these identities is essential for solving more complex trigonometric problems.
-
Solving Oblique Triangles: These are triangles that don't have a right angle. Specialized trigonometric laws, such as the Law of Sines and the Law of Cosines, are used to solve oblique triangles.
-
Inverse Trigonometric Functions: These functions allow us to find the angle when we know the trigonometric ratio of the angle. For example, if sin A = 0.5, then A = sin⁻¹(0.5) = 30°.
-
Trigonometric Graphs: Understanding the graphs of sine, cosine, and tangent functions is crucial for various applications, including modeling periodic phenomena.
Conclusion: Mastering Trigonometric Ratios for Success
Mastering trigonometric ratios is a cornerstone of success in mathematics and various STEM fields. By understanding the relationships between angles and sides in right-angled triangles, and applying the sine, cosine, and tangent ratios effectively, you can solve a wide range of problems. Remember to practice consistently, working through different scenarios and applying the concepts to real-world examples to solidify your understanding. As you progress, explore the more advanced concepts to expand your trigonometric knowledge and unlock a world of applications in mathematics, science, and engineering. Consistent practice and a methodical approach will ensure you can confidently tackle any trigonometric challenge that comes your way. The journey to mastering trigonometry is rewarding; embrace the challenge, and enjoy the process of unlocking the fascinating world of angles and triangles.
Latest Posts
Latest Posts
-
Section 2 Topic 5 Solving Inequalities Part 1
Mar 29, 2025
-
Summary Of The Giver Chapter 20
Mar 29, 2025
-
Quotes From When The Emperor Was Divine
Mar 29, 2025
-
Medical Decision Making Is Based On Which Of The Following
Mar 29, 2025
-
How Many Chapters Are In The Handmaids Tale
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Homework 4 Trigonometric Ratios & Finding Missing Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
