Is 0 0 A Solution To This System
Onlines
Mar 28, 2025 · 5 min read
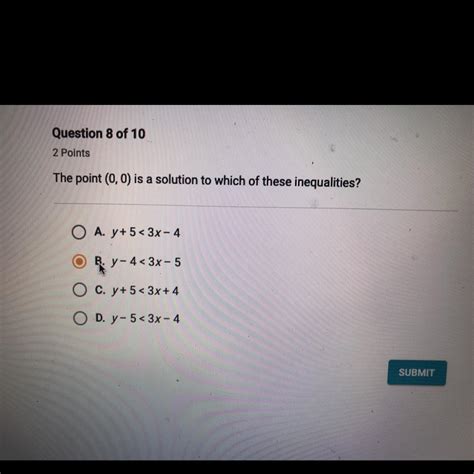
Table of Contents
Is (0, 0) a Solution to This System? A Comprehensive Guide to Linear Equations
Determining whether (0, 0) is a solution to a given system of linear equations is a fundamental concept in algebra. This seemingly simple question underpins a deeper understanding of linear systems, their graphical representations, and their applications in various fields. This article will explore this question in detail, examining different types of systems, methods for solving them, and the implications of (0, 0) as a solution.
Understanding Linear Equations and Systems
A linear equation is an equation that can be written in the form ax + by = c, where 'a', 'b', and 'c' are constants, and 'x' and 'y' are variables. The graph of a linear equation is a straight line.
A system of linear equations involves two or more linear equations with the same variables. The solution to a system of linear equations is the set of values for the variables that satisfy all equations simultaneously. Graphically, this represents the point(s) of intersection between the lines.
Checking if (0, 0) is a Solution
To determine if (0, 0) is a solution to a system of linear equations, simply substitute x = 0 and y = 0 into each equation in the system. If the equations hold true for these values, then (0, 0) is a solution; otherwise, it is not.
Example 1:
Consider the system:
- 2x + 3y = 0
- x - y = 0
Substituting x = 0 and y = 0 into the first equation:
2(0) + 3(0) = 0
This simplifies to 0 = 0, which is true.
Substituting x = 0 and y = 0 into the second equation:
0 - 0 = 0
This also simplifies to 0 = 0, which is true.
Since both equations are true when x = 0 and y = 0, (0, 0) is a solution to this system.
Example 2:
Consider the system:
- x + 2y = 5
- 3x - y = 2
Substituting x = 0 and y = 0 into the first equation:
0 + 2(0) = 5
This simplifies to 0 = 5, which is false.
There's no need to check the second equation; since the first equation is false, (0, 0) is not a solution to this system.
Types of Linear Systems and (0, 0) as a Solution
The nature of the solution to a system of linear equations depends on the relationship between the lines represented by the equations. There are three possibilities:
- Consistent and Independent: The lines intersect at exactly one point. (0, 0) might be this point, or it might not.
- Consistent and Dependent: The lines are coincident (overlap completely). This means there are infinitely many solutions, and (0, 0) could be one of them.
- Inconsistent: The lines are parallel and never intersect. There is no solution to the system, and (0, 0) cannot be a solution.
Consistent and Dependent Systems and (0, 0):
In a consistent and dependent system, the equations are essentially multiples of each other. For example:
- x + y = 0
- 2x + 2y = 0
Both equations represent the same line. (0, 0) lies on this line, so it's one of the infinitely many solutions.
Inconsistent Systems and (0, 0):
Parallel lines never intersect, so there's no common solution. For example:
- x + y = 1
- x + y = 2
These lines are parallel; therefore, there is no solution, and (0, 0) is definitely not a solution.
Graphical Interpretation
Graphically, the point (0, 0) represents the origin of the coordinate plane. If the lines representing the equations in the system intersect at the origin, then (0, 0) is a solution.
Solving Systems of Linear Equations
Several methods can be used to solve systems of linear equations:
- Substitution: Solve one equation for one variable, then substitute that expression into the other equation.
- Elimination: Multiply equations by constants to eliminate one variable when adding the equations together.
- Graphical Method: Graph both equations and find the point of intersection.
The choice of method depends on the specific system and personal preference. However, regardless of the method, the result will be the same – the set of values that satisfy all equations.
Applications of Linear Systems
Linear systems have numerous applications in various fields, including:
- Engineering: Analyzing circuits, structural mechanics, and control systems.
- Economics: Modeling supply and demand, input-output analysis, and linear programming.
- Computer Science: Computer graphics, image processing, and machine learning.
- Physics: Solving problems related to forces, motion, and electricity.
Understanding whether (0, 0) is a solution to a given linear system provides valuable insights into the behaviour and properties of that system within the context of its application.
Advanced Considerations: Matrices and Determinants
For larger systems of linear equations (more than two variables), matrix methods are often used. The determinant of the coefficient matrix plays a crucial role in determining the nature of the solution:
- A non-zero determinant indicates a unique solution (consistent and independent).
- A zero determinant indicates either infinitely many solutions (consistent and dependent) or no solution (inconsistent).
Even in these more complex cases, determining if (0, 0) is a solution simply involves substituting x = 0, y = 0, and so on into the equations.
Conclusion: The Significance of (0, 0)
While seemingly a trivial question, determining whether (0, 0) is a solution to a system of linear equations provides a valuable foundational understanding of linear algebra and its applications. It highlights the relationship between algebraic manipulation and graphical representation, offering insights into the behavior and solutions of linear systems. Whether (0, 0) is a solution depends entirely on the specific equations in the system and can only be determined by direct substitution or through a complete solution process. This seemingly simple problem offers a gateway to a deeper understanding of a powerful mathematical tool. The significance extends beyond simple exercises to encompass real-world applications where determining if the origin (0, 0) is a solution has important implications for the modelled system.
Latest Posts
Latest Posts
-
Alan Smith Physical Therapist Kansas Npi Number
Mar 31, 2025
-
Practice Complex Inheritance Patterns Answer Key
Mar 31, 2025
-
The Guest Summary By Albert Camus
Mar 31, 2025
-
The Great Gatsby Student Workbook Answer Key Pdf
Mar 31, 2025
-
Statement Of Cash Flows For Snowdrop A Limited Company
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Is 0 0 A Solution To This System . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
