The Rectangular Homogeneous Gate Shown Below Is
Onlines
Apr 01, 2025 · 6 min read
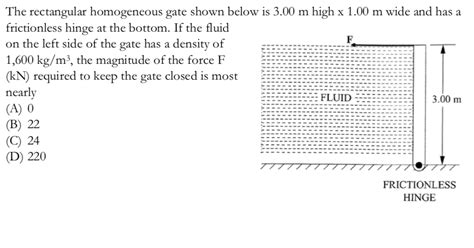
Table of Contents
Analyzing the Rectangular Homogeneous Gate: Forces, Moments, and Stability
The analysis of a rectangular homogeneous gate, often encountered in engineering mechanics and structural analysis, involves understanding the forces acting upon it, calculating the resultant moments, and ultimately determining its stability. This in-depth article will explore these aspects, providing a comprehensive guide for engineers and students alike. We'll delve into the principles of fluid statics, center of pressure calculation, and stability criteria, illustrating concepts with practical examples and clarifying potential points of confusion.
Understanding the Forces at Play
A rectangular homogeneous gate submerged in a fluid experiences several key forces:
-
Hydrostatic Pressure: This is the primary force acting on the gate, stemming from the fluid's weight. The pressure increases linearly with depth, meaning the pressure at the bottom of the gate is significantly greater than at the top. This pressure acts perpendicular to the gate's surface at every point.
-
Weight of the Gate: This is a vertical force acting downwards, concentrated at the gate's center of gravity. The magnitude of this force depends on the gate's density and volume.
-
Reaction Forces: These are the forces exerted by the hinges or supports holding the gate in place. These forces are reactive, meaning they oppose the other forces acting on the gate to maintain equilibrium. Their direction and magnitude depend on the gate's geometry, fluid pressure distribution, and its weight.
Calculating Hydrostatic Pressure
The pressure at any point within a fluid is given by the formula:
P = ρgh
Where:
- P is the pressure (Pascals)
- ρ is the fluid density (kg/m³)
- g is the acceleration due to gravity (m/s²)
- h is the depth of the point below the fluid surface (m)
To determine the total hydrostatic force acting on the gate, we need to integrate the pressure over the gate's submerged area. For a rectangular gate, this integration simplifies to:
F = (1/2)ρgwh²
Where:
- F is the total hydrostatic force (N)
- w is the width of the gate (m)
- h is the depth of the submerged portion of the gate (m)
This equation represents the total force exerted by the fluid on the gate. Note that this force acts at the centroid of the submerged area, which is not the same as the center of pressure.
Locating the Center of Pressure
The center of pressure is the point where the resultant hydrostatic force acts. For a rectangular gate, the center of pressure is located at a depth of (2/3)h below the surface of the fluid. This is different from the centroid of the submerged area which is at a depth of (1/2)h. This difference arises from the non-uniform pressure distribution on the gate. Knowing the location of the center of pressure is crucial for calculating the moments.
Calculating the exact location of the center of pressure involves a moment calculation. The total moment about the surface of the fluid is equal to the hydrostatic force multiplied by the distance from the surface to the center of pressure (y_cp). This leads to the following equation:
y_cp = (2/3)h
This shows that the center of pressure is always located below the centroid of the submerged area.
Calculating Moments and Determining Stability
Once we've determined the hydrostatic force and its location (center of pressure), we can calculate the moment exerted by this force about the hinges or supports. The moment is simply the force multiplied by the perpendicular distance from the line of action of the force to the hinge point.
The gate's stability depends on the balance of moments. If the moment due to the hydrostatic force is greater than the moment due to the gate's weight, then the gate will rotate and potentially open. Conversely, if the moment due to the gate's weight is greater, the gate will remain closed.
The stability can also be assessed by calculating the reaction forces at the hinges. If the reaction forces are within the permissible limits of the hinges' material strength, then the gate is considered stable. Otherwise, failure may occur.
Factors Influencing Gate Stability
Several factors can influence the stability of a rectangular homogeneous gate:
-
Fluid Density: A higher fluid density leads to a greater hydrostatic force, increasing the tendency for the gate to open.
-
Gate Dimensions: The width, height, and submerged depth of the gate directly influence the hydrostatic force and moments.
-
Gate Material and Weight: A heavier gate, due to its material density and dimensions, can help resist the opening moment of the hydrostatic force.
-
Hinge Location: The location of the hinges plays a significant role. If the hinges are closer to the bottom of the gate, the opening moment due to hydrostatic pressure will be reduced.
-
External Forces: Any additional external forces acting on the gate, such as wind or waves, will affect the overall moment balance and stability.
Practical Applications and Examples
The principles discussed here find applications in various engineering scenarios:
-
Dam Design: Understanding hydrostatic pressure and gate stability is critical in designing safe and reliable dams. Gates are essential for controlling water levels and releasing excess water during floods.
-
Hydraulic Structures: Various hydraulic structures, such as spillways and sluice gates, rely on a thorough understanding of the forces acting on gates to ensure their stability and functionality.
-
Lock Gates: Canal lock gates are designed to withstand significant hydrostatic pressure differentials as ships pass through the locks. The design ensures that the gates remain closed under pressure.
-
Water Tanks and Reservoirs: Large water tanks and reservoirs sometimes employ gates for controlling water levels or emptying purposes. The analysis of such gates is crucial for safety and operation.
Advanced Considerations
In real-world scenarios, more complex factors might come into play:
-
Gate Deflection: The gate may not remain perfectly rigid; it might deflect slightly under the load. This deflection can affect the moment calculations.
-
Fluid Viscosity: In some cases, the fluid's viscosity could influence the pressure distribution on the gate.
-
Dynamic Effects: If the fluid level or the gate's position changes rapidly, dynamic effects must be considered.
Conclusion
The analysis of a rectangular homogeneous gate is a fundamental problem in engineering mechanics. Understanding the principles of hydrostatic pressure, calculating the center of pressure, and analyzing moments and stability are crucial skills for engineers involved in designing and analyzing hydraulic structures. By carefully considering all factors and employing appropriate analytical techniques, engineers can ensure the safe and reliable operation of these essential components in various applications. This in-depth understanding allows engineers to design robust and efficient systems that withstand the forces of nature and serve their intended purpose. Further exploration into advanced topics like fluid dynamics and structural analysis will provide a more comprehensive understanding of the complexities involved in designing and managing such systems.
Latest Posts
Latest Posts
-
Which Trait Of Mycenaean Architecture Is Represented In This Image
Apr 02, 2025
-
Label The Structures Of The Pericardium In The Figure
Apr 02, 2025
-
Jeff Nippard High Frequency Full Body Pdf
Apr 02, 2025
-
Hc D 1 3 Material Presents What Type Of Hazard
Apr 02, 2025
-
Jimena Limpia El Congelador Jimena Esta En
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about The Rectangular Homogeneous Gate Shown Below Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
