Topic 2.8 Inverse Functions Answer Key
Onlines
Mar 27, 2025 · 4 min read
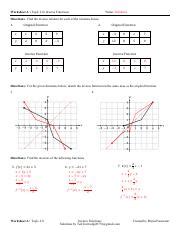
Table of Contents
Topic 2.8: Inverse Functions – A Comprehensive Guide with Answer Key
Understanding inverse functions is crucial for mastering algebra and precalculus. This comprehensive guide will delve into the concept of inverse functions, providing a detailed explanation, examples, and a complete answer key for practice problems. We'll explore how to find inverse functions, verify them, and understand their graphical representation. Let's dive in!
What are Inverse Functions?
An inverse function essentially "undoes" what the original function does. If a function f maps an input x to an output y, its inverse function, denoted as f<sup>-1</sup>(x) (read as "f inverse of x"), maps that output y back to the original input x. This is only possible if the original function is one-to-one (also known as injective), meaning each input has a unique output, and vice versa. If a function is not one-to-one, you can sometimes restrict its domain to create a one-to-one function that allows for an inverse.
Key Characteristic: The composition of a function and its inverse results in the identity function, meaning f(f<sup>-1</sup>(x)) = x and f<sup>-1</sup>(f(x)) = x.
How to Find the Inverse of a Function
Finding the inverse of a function involves a systematic process:
-
Replace f(x) with y: This simplifies the notation.
-
Swap x and y: This is the crucial step that reverses the mapping.
-
Solve for y: Algebraically manipulate the equation to isolate y.
-
Replace y with f<sup>-1</sup>(x): This denotes the inverse function.
Example 1: Find the inverse of f(x) = 2x + 3.
- y = 2x + 3
- x = 2y + 3
- x - 3 = 2y
- y = (x - 3) / 2
- Therefore, f<sup>-1</sup>(x) = (x - 3) / 2
Example 2: Find the inverse of f(x) = x² (for x ≥ 0). Notice the restriction on the domain. Without it, the function wouldn't be one-to-one.
- y = x²
- x = y²
- y = ±√x
- Since x ≥ 0, we only consider the positive square root.
- Therefore, f<sup>-1</sup>(x) = √x
Verifying Inverse Functions
After finding the inverse, it's essential to verify your result. This is done by checking if the compositions f(f<sup>-1</sup>(x)) = x and f<sup>-1</sup>(f(x)) = x hold true.
Example 3: Verify the inverse found in Example 1.
f(f<sup>-1</sup>(x)) = f((x - 3) / 2) = 2((x - 3) / 2) + 3 = x - 3 + 3 = x
f<sup>-1</sup>(f(x)) = f<sup>-1</sup>(2x + 3) = ((2x + 3) - 3) / 2 = 2x / 2 = x
Since both compositions result in x, the inverse function is correctly found.
Graphical Representation of Inverse Functions
The graphs of a function and its inverse are reflections of each other across the line y = x. This is because swapping x and y in the equation corresponds to a reflection about the line y = x.
Common Mistakes to Avoid
-
Forgetting to swap x and y: This is the most frequent error. Remember, this step is the core of finding the inverse.
-
Incorrect algebraic manipulation: Carefully solve for y to avoid errors. Check your steps.
-
Ignoring domain restrictions: If the original function isn't one-to-one, restrict its domain to make it so before finding the inverse.
-
Not verifying the inverse: Always verify your solution to ensure accuracy.
Practice Problems with Answer Key
Now, let's test your understanding with some practice problems. Remember to follow the steps outlined above.
Problem 1: Find the inverse of f(x) = 5x - 7.
Problem 2: Find the inverse of f(x) = (x + 2) / 3.
Problem 3: Find the inverse of f(x) = x³ + 1.
Problem 4: Find the inverse of f(x) = √(x - 4) (for x ≥ 4).
Problem 5: Find the inverse of f(x) = 1/x (for x ≠ 0).
Problem 6: Find the inverse of f(x) = 2<sup>x</sup>. (Hint: Consider logarithmic functions)
Problem 7: Verify your answer for Problem 1.
Problem 8: Verify your answer for Problem 4.
Answer Key
Problem 1: f<sup>-1</sup>(x) = (x + 7) / 5
Problem 2: f<sup>-1</sup>(x) = 3x - 2
Problem 3: f<sup>-1</sup>(x) = ∛(x - 1)
Problem 4: f<sup>-1</sup>(x) = x² + 4 (for x ≥ 0)
Problem 5: f<sup>-1</sup>(x) = 1/x (for x ≠ 0) (Notice that the inverse is the same as the original function!)
Problem 6: f<sup>-1</sup>(x) = log₂(x) (for x > 0)
Problem 7: Verification: f(f<sup>-1</sup>(x)) = 5((x + 7) / 5) - 7 = x + 7 - 7 = x f<sup>-1</sup>(f(x)) = ((5x - 7) + 7) / 5 = 5x / 5 = x
Problem 8: Verification: f(f<sup>-1</sup>(x)) = √((x² + 4) - 4) = √(x²) = x (for x ≥ 0) f<sup>-1</sup>(f(x)) = (√(x - 4))² + 4 = x - 4 + 4 = x (for x ≥ 4)
Conclusion
Mastering inverse functions is a cornerstone of advanced mathematical concepts. By understanding the process, verifying your results, and practicing regularly, you'll build a strong foundation for future studies in calculus and beyond. Remember to always check your work and pay attention to domain restrictions. Practice these problems diligently, and refer back to this guide as needed. Good luck!
Latest Posts
Latest Posts
-
Identify The Statements That Correctly Describe The Site Of Bouri
Mar 30, 2025
-
Pal Histology Muscular Tissue Lab Practical Question 9
Mar 30, 2025
-
La Natacion Bucear Esquiar El Parque
Mar 30, 2025
-
Peptic Ulcer Disease Hesi Case Study
Mar 30, 2025
-
A Covered Entity Must Have An Established Complaint Process
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Topic 2.8 Inverse Functions Answer Key . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
