Unit 8 Homework 6 Trigonometry Review
Onlines
Apr 08, 2025 · 5 min read
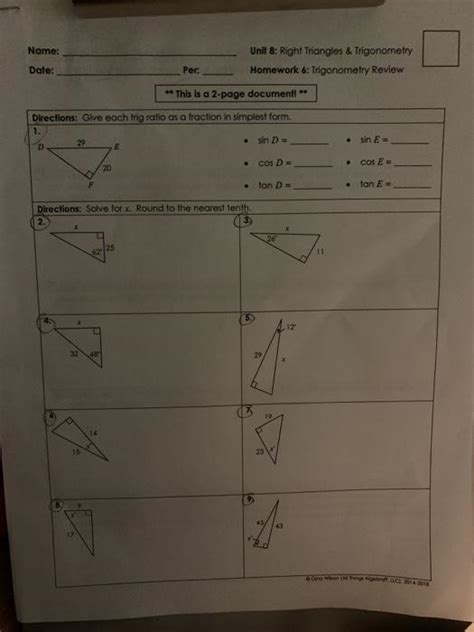
Table of Contents
Unit 8 Homework 6: Trigonometry Review – A Comprehensive Guide
This comprehensive guide delves into the key concepts covered in Unit 8, Homework 6, focusing on a trigonometry review. We'll explore fundamental trigonometric functions, their applications, and problem-solving strategies to help you ace your assignment. This guide aims to provide a thorough understanding, going beyond simple answers and focusing on the underlying principles.
Understanding the Trigonometric Functions
Trigonometry, at its core, studies the relationships between angles and sides of triangles. The three primary trigonometric functions – sine, cosine, and tangent – are defined in the context of a right-angled triangle.
Defining Sine, Cosine, and Tangent
Consider a right-angled triangle with a hypotenuse (the side opposite the right angle), an opposite side (the side opposite a given angle), and an adjacent side (the side next to the given angle). The trigonometric functions are defined as follows:
- Sine (sin): sin(θ) = opposite / hypotenuse
- Cosine (cos): cos(θ) = adjacent / hypotenuse
- Tangent (tan): tan(θ) = opposite / adjacent
Where θ represents the angle of interest.
Understanding the Unit Circle
Beyond right-angled triangles, trigonometric functions extend to all angles using the unit circle. The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. Any point on the unit circle can be represented by its coordinates (x, y), which are related to the cosine and sine of the angle formed by the positive x-axis and the line connecting the origin to that point.
- x-coordinate: cos(θ)
- y-coordinate: sin(θ)
This representation allows us to define trigonometric functions for angles beyond 0° to 90°.
Reciprocal Trigonometric Functions
Three additional trigonometric functions are defined as the reciprocals of the primary functions:
- Cosecant (csc): csc(θ) = 1/sin(θ) = hypotenuse / opposite
- Secant (sec): sec(θ) = 1/cos(θ) = hypotenuse / adjacent
- Cotangent (cot): cot(θ) = 1/tan(θ) = adjacent / opposite
Solving Trigonometric Problems: A Step-by-Step Approach
Solving trigonometry problems often involves applying these functions to find unknown sides or angles in triangles or using the unit circle to determine values for specific angles. Let's break down a systematic approach.
Right-Angled Triangle Problems
- Identify the knowns and unknowns: Determine which sides and angles are given and which need to be calculated.
- Choose the appropriate trigonometric function: Select the function that relates the known and unknown quantities. For example, if you know the opposite side and the hypotenuse and need to find an angle, use the sine function.
- Set up the equation: Substitute the known values into the chosen trigonometric function.
- Solve for the unknown: Use algebraic manipulation to solve for the unknown side or angle. Remember to use inverse trigonometric functions (arcsin, arccos, arctan) to find angles.
- Check your answer: Ensure your answer is reasonable within the context of the problem.
Unit Circle Problems
- Determine the angle: Identify the angle in question, considering its location on the unit circle (quadrant, reference angle).
- Identify the relevant coordinates: Use the angle to determine the x and y coordinates on the unit circle. Remember the signs of the coordinates in each quadrant.
- Calculate the trigonometric function: Use the x and y coordinates to calculate the sine, cosine, and tangent of the angle. For example, sin(θ) = y-coordinate and cos(θ) = x-coordinate.
- Consider the reciprocal functions: If necessary, calculate the cosecant, secant, and cotangent using the reciprocal relationships.
Example Problems
Let's work through a couple of example problems to illustrate these concepts.
Example 1: Right-Angled Triangle
A right-angled triangle has a hypotenuse of 10 cm and an angle of 30°. Find the length of the side opposite the 30° angle.
- Knowns: Hypotenuse = 10 cm, angle = 30°
- Unknown: Opposite side
- Function: We use sine since sin(θ) = opposite / hypotenuse
- Equation: sin(30°) = opposite / 10
- Solution: opposite = 10 * sin(30°) = 10 * 0.5 = 5 cm
Example 2: Unit Circle
Find the value of sin(150°).
- Angle: 150° lies in the second quadrant.
- Reference Angle: The reference angle is 180° - 150° = 30°
- Coordinates: In the second quadrant, the x-coordinate is negative, and the y-coordinate is positive. Therefore, the coordinates are approximately (-√3/2, 1/2).
- Sine: sin(150°) = y-coordinate = 1/2
Advanced Trigonometry Concepts
This section will introduce some more advanced concepts often encountered in higher-level trigonometry.
Trigonometric Identities
Trigonometric identities are equations that are true for all values of the involved angles. They are crucial for simplifying expressions and solving more complex trigonometric equations. Some important identities include:
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1
- Tangent Identity: tan(θ) = sin(θ) / cos(θ)
- Sum and Difference Identities: These identities provide formulas for finding the sine, cosine, and tangent of the sum or difference of two angles.
- Double-Angle Identities: These identities express trigonometric functions of 2θ in terms of functions of θ.
Solving Trigonometric Equations
Solving trigonometric equations involves finding the values of the angle(θ) that satisfy a given equation. Techniques include using trigonometric identities to simplify the equation, factoring, and using inverse trigonometric functions.
Graphing Trigonometric Functions
Graphing trigonometric functions provides a visual representation of their periodic nature. Understanding the amplitude, period, phase shift, and vertical shift allows for accurate sketching of sine, cosine, and tangent graphs.
Tips for Success in Trigonometry
- Master the basics: Ensure a strong understanding of the fundamental definitions and relationships before moving on to more complex concepts.
- Practice regularly: Consistent practice is key to mastering trigonometry. Work through numerous problems of varying difficulty.
- Use visual aids: Diagrams and the unit circle can be invaluable tools for visualizing trigonometric relationships.
- Seek help when needed: Don't hesitate to ask for assistance from teachers, tutors, or classmates if you're struggling with any concepts.
- Review regularly: Consistent review helps solidify your understanding and prevents forgetting key concepts.
Conclusion
This in-depth guide provides a solid foundation for tackling Unit 8, Homework 6: Trigonometry Review. By understanding the fundamental concepts, mastering problem-solving techniques, and practicing regularly, you'll be well-prepared to excel in your assignment and further studies in trigonometry. Remember that consistent effort and a methodical approach are essential to success in this field. Good luck!
Latest Posts
Latest Posts
-
Simulation Lab 10 2 Module 10 Install Linux In Vm
Apr 08, 2025
-
Data Nugget City Parks Answer Key
Apr 08, 2025
-
Building A Forensic Workstation Is More Expensive Than Purchasing One
Apr 08, 2025
-
How Does Caring Help Establish Credibility In The Business World
Apr 08, 2025
-
End Of Semester Test Geometry Semester A
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Unit 8 Homework 6 Trigonometry Review . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.