Using Reaction Free Energy To Predict Equilibrium Composition
Onlines
Mar 28, 2025 · 6 min read
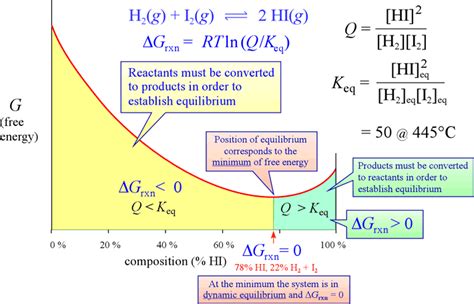
Table of Contents
Using Reaction Free Energy to Predict Equilibrium Composition
Determining the equilibrium composition of a chemical reaction is crucial in various fields, from industrial chemical processes to environmental modeling. While experimental methods provide valuable data, theoretical predictions using reaction free energy offer a powerful and efficient alternative, particularly for complex systems or scenarios where experiments are difficult or costly to conduct. This article delves into the principles behind using reaction free energy to predict equilibrium composition, exploring different approaches and their applications.
Understanding Gibbs Free Energy and Equilibrium
The cornerstone of predicting equilibrium composition is the Gibbs Free Energy (ΔG). This thermodynamic potential quantifies the maximum reversible work that can be performed by a system at constant temperature and pressure. For a chemical reaction, the change in Gibbs Free Energy (ΔG<sub>rxn</sub>) determines the spontaneity and extent of the reaction.
Key Relationships:
- ΔG<sub>rxn</sub> < 0: The reaction is spontaneous in the forward direction; products are favored at equilibrium.
- ΔG<sub>rxn</sub> > 0: The reaction is non-spontaneous in the forward direction; reactants are favored at equilibrium.
- ΔG<sub>rxn</sub> = 0: The reaction is at equilibrium; the rates of the forward and reverse reactions are equal.
At equilibrium, the change in Gibbs Free Energy is zero (ΔG<sub>rxn</sub> = 0). This fundamental principle allows us to predict the equilibrium composition by relating ΔG<sub>rxn</sub> to the equilibrium constant (K<sub>eq</sub>).
The Relationship Between ΔG<sub>rxn</sub> and K<sub>eq</sub>
The standard Gibbs free energy change (ΔG°<sub>rxn</sub>) is related to the equilibrium constant (K<sub>eq</sub>) through the following equation:
ΔG°<sub>rxn</sub> = -RTlnK<sub>eq</sub>
Where:
- R is the ideal gas constant (8.314 J/mol·K)
- T is the temperature in Kelvin
This equation is a powerful tool. Knowing the standard Gibbs free energy change for a reaction allows us to calculate the equilibrium constant, which directly relates to the equilibrium concentrations of reactants and products.
Calculating ΔG<sub>rxn</sub> and Predicting Equilibrium Composition
Several methods are available for calculating ΔG<sub>rxn</sub>, each with its own advantages and limitations:
1. Using Standard Free Energy of Formation (ΔG°<sub>f</sub>)
This is a common approach, especially for reactions involving simple molecules. The standard free energy of formation (ΔG°<sub>f</sub>) is the change in Gibbs free energy when one mole of a compound is formed from its constituent elements in their standard states (usually 298 K and 1 atm). ΔG°<sub>rxn</sub> can then be calculated using the following equation:
ΔG°<sub>rxn</sub> = Σ ΔG°<sub>f</sub>(products) - Σ ΔG°<sub>f</sub>(reactants)
This method requires access to tabulated standard free energy of formation values, readily available in thermodynamic databases.
2. Using Enthalpy (ΔH) and Entropy (ΔS) Changes
The Gibbs free energy is related to enthalpy (ΔH) and entropy (ΔS) changes through the following equation:
ΔG = ΔH - TΔS
This approach is particularly useful when ΔH and ΔS values are known or can be estimated, for example, using computational methods such as density functional theory (DFT) calculations. This allows for the prediction of equilibrium compositions at different temperatures.
3. Computational Chemistry Methods
Advanced computational chemistry techniques, such as DFT and ab initio methods, can be employed to calculate the energies of reactants and products directly. These methods provide highly accurate results but require significant computational resources and expertise.
Equilibrium Constant and Equilibrium Composition: The Connection
The equilibrium constant (K<sub>eq</sub>) is a dimensionless quantity that reflects the relative amounts of reactants and products at equilibrium. For a general reaction:
aA + bB ⇌ cC + dD
The equilibrium constant is defined as:
K<sub>eq</sub> = ([C]<sup>c</sup>[D]<sup>d</sup>) / ([A]<sup>a</sup>[B]<sup>b</sup>)
where [A], [B], [C], and [D] represent the equilibrium concentrations of the respective species. By combining the equation relating ΔG°<sub>rxn</sub> and K<sub>eq</sub> with the equilibrium constant expression, we can determine the equilibrium concentrations of reactants and products, given initial conditions and the standard Gibbs free energy change. For complex reactions, numerical methods or iterative calculations may be necessary to solve for the equilibrium concentrations.
Factors Affecting Equilibrium Composition
Several factors influence the equilibrium composition of a reaction:
-
Temperature: Changing the temperature alters the equilibrium constant, and consequently, the equilibrium concentrations. The effect of temperature depends on the enthalpy change (ΔH) of the reaction. Exothermic reactions (ΔH < 0) shift to the left (favoring reactants) with increasing temperature, while endothermic reactions (ΔH > 0) shift to the right (favoring products).
-
Pressure: For reactions involving gases, changing the pressure affects the equilibrium composition. Increasing pressure favors the side with fewer moles of gas, while decreasing pressure favors the side with more moles of gas.
-
Concentration: Changing the concentration of reactants or products will shift the equilibrium to counteract the change (Le Chatelier's principle).
Applications of Predicting Equilibrium Composition
The ability to predict equilibrium composition using reaction free energy has broad applications across various fields:
1. Chemical Engineering: Process Optimization
Predicting equilibrium composition is critical for optimizing chemical processes. It helps determine the optimal reaction conditions (temperature, pressure, reactant ratios) to maximize product yield and minimize waste. This is crucial for designing efficient and cost-effective industrial processes.
2. Environmental Science: Pollution Control
Understanding equilibrium compositions is essential for modeling and predicting pollutant behavior in environmental systems. It helps assess the fate and transport of pollutants and design effective remediation strategies.
3. Materials Science: Synthesis and Characterization
Predicting equilibrium compositions is valuable in materials science for designing and synthesizing new materials with desired properties. It enables researchers to optimize reaction conditions to achieve the target composition and microstructure.
4. Biochemistry: Metabolic Pathways
In biochemistry, predicting equilibrium compositions helps understand metabolic pathways and the regulation of enzyme activity. It provides insights into the efficiency of biochemical reactions and the distribution of metabolites in cells and organisms.
5. Geochemistry: Mineral Formation and Weathering
Geochemists use these principles to model mineral formation and weathering processes. Predicting equilibrium compositions helps understand the distribution of elements in the Earth's crust and predict the long-term fate of geological materials.
Limitations and Considerations
While predicting equilibrium composition using reaction free energy is a powerful tool, several limitations and considerations exist:
-
Ideal conditions: The calculations often assume ideal conditions (ideal gas behavior, negligible intermolecular interactions), which may not always be valid in real-world scenarios. Activity coefficients may need to be incorporated for non-ideal solutions.
-
Reaction kinetics: The thermodynamic approach predicts equilibrium composition but does not provide information about the rate at which equilibrium is reached. Kinetic limitations can significantly affect the actual composition in a given timeframe.
-
Accuracy of data: The accuracy of the predictions depends on the accuracy of the thermodynamic data used (ΔG°<sub>f</sub>, ΔH, ΔS). Using reliable and validated data is crucial.
-
Complex reactions: For complex reactions involving multiple equilibria and side reactions, the calculations can become quite challenging and require advanced numerical methods.
Conclusion
Predicting equilibrium composition using reaction free energy offers a powerful and versatile approach for understanding and optimizing chemical systems. By understanding the relationships between Gibbs free energy, equilibrium constants, and equilibrium concentrations, researchers and engineers can gain valuable insights into the behavior of chemical reactions under various conditions. While limitations exist, the ongoing advancements in computational chemistry and thermodynamic databases are constantly expanding the accuracy and applicability of this essential technique across numerous scientific and engineering disciplines. The ability to accurately predict equilibrium compositions is instrumental in optimizing chemical processes, understanding environmental systems, designing new materials, and furthering our knowledge of fundamental chemical principles.
Latest Posts
Latest Posts
-
Label The Illustrations Based On The Gestalt Principles Of Grouping
Mar 31, 2025
-
Those Who Oppose Corporate Social Responsibility Believe That
Mar 31, 2025
-
5 08 Quiz Operations With Rational Expressions
Mar 31, 2025
-
Companies With Strong Safety Cultures Usually Have Lower
Mar 31, 2025
-
Limpiar Un Poco Antes De Hacer Las Diligencias
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Using Reaction Free Energy To Predict Equilibrium Composition . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
