Volume Of Prisms And Cylinders Maze Answer Key
Onlines
Mar 28, 2025 · 5 min read
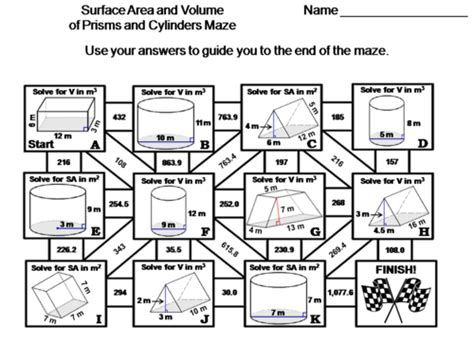
Table of Contents
Volume of Prisms and Cylinders Maze: Answer Key and Comprehensive Guide
This comprehensive guide provides the answer key to a volume of prisms and cylinders maze, along with detailed explanations and supplemental information to solidify your understanding of these geometric concepts. We'll explore the formulas, tackle different prism and cylinder types, and offer strategies for solving similar problems. This guide is perfect for students, teachers, and anyone looking to master the calculation of volumes.
Understanding Volume: The Basics
Before diving into the maze, let's establish a strong foundation in understanding volume. Volume refers to the amount of three-dimensional space occupied by an object. For prisms and cylinders, we're essentially calculating the space enclosed within their boundaries.
Key Terms:
- Prism: A three-dimensional solid with two parallel and congruent bases connected by rectangular lateral faces. Prisms are named according to the shape of their base (e.g., rectangular prism, triangular prism, pentagonal prism).
- Cylinder: A three-dimensional solid with two parallel and congruent circular bases connected by a curved lateral surface.
- Base: The two congruent and parallel faces of a prism or cylinder.
- Height (h): The perpendicular distance between the two bases of a prism or cylinder.
- Area (A): The two-dimensional space enclosed within a shape. In the context of volume calculations, we frequently use the area of the base.
Volume Formulas: The Cornerstones of Calculation
The formulas for calculating the volume of prisms and cylinders are fundamental to solving the maze and related problems.
Volume of a Prism:
The volume (V) of any prism is calculated using the following formula:
V = Area of the base (A<sub>base</sub>) × Height (h)
This formula emphasizes that the volume is essentially the area of the base multiplied by the height. The area of the base will vary depending on the shape of the base (rectangle, triangle, pentagon, etc.).
Examples:
- Rectangular Prism: A<sub>base</sub> = length × width; V = length × width × height
- Triangular Prism: A<sub>base</sub> = (1/2) × base × height of triangle; V = (1/2) × base × height of triangle × height of prism
- Pentagonal Prism: A<sub>base</sub> (requires more complex calculation, often breaking the pentagon into triangles); V = A<sub>base</sub> × height of prism
Volume of a Cylinder:
The volume (V) of a cylinder is calculated using the following formula:
V = πr²h
Where:
- π (pi): Approximately 3.14159
- r: Radius of the circular base
- h: Height of the cylinder
This formula uses the area of the circular base (πr²) multiplied by the height.
Solving the Volume of Prisms and Cylinders Maze: A Step-by-Step Approach
Now, let's tackle the maze. Without the visual maze itself, I'll provide a general approach and illustrate with example problems. The maze likely presents a series of problems requiring volume calculations, with the correct answers leading to the exit.
General Strategy:
- Identify the shape: Determine if the problem involves a prism or a cylinder.
- Identify the necessary dimensions: Determine the height and the dimensions needed to calculate the area of the base.
- Calculate the area of the base: Use the appropriate formula based on the shape of the base.
- Calculate the volume: Use the appropriate formula for the volume of a prism or cylinder.
- Compare your answer to the choices: Select the path corresponding to the correct answer.
Example Problems and Solutions:
Problem 1: A rectangular prism has a length of 5 cm, a width of 3 cm, and a height of 4 cm. What is its volume?
Solution:
- Shape: Rectangular prism
- Dimensions: length = 5 cm, width = 3 cm, height = 4 cm
- Area of base: A<sub>base</sub> = length × width = 5 cm × 3 cm = 15 cm²
- Volume: V = A<sub>base</sub> × h = 15 cm² × 4 cm = 60 cm³
- Answer: 60 cm³
Problem 2: A cylinder has a radius of 2 cm and a height of 7 cm. What is its volume?
Solution:
- Shape: Cylinder
- Dimensions: radius (r) = 2 cm, height (h) = 7 cm
- Area of base: A<sub>base</sub> = πr² = π(2 cm)² = 4π cm²
- Volume: V = πr²h = 4π cm² × 7 cm = 28π cm³ (approximately 87.96 cm³)
- Answer: 28π cm³ (or approximately 87.96 cm³)
Problem 3: A triangular prism has a base triangle with a base of 6 cm and a height of 4 cm. The height of the prism is 10 cm. What is its volume?
Solution:
- Shape: Triangular prism
- Dimensions: Base of triangle = 6 cm, Height of triangle = 4 cm, Height of prism = 10 cm
- Area of base: A<sub>base</sub> = (1/2) × base × height = (1/2) × 6 cm × 4 cm = 12 cm²
- Volume: V = A<sub>base</sub> × h = 12 cm² × 10 cm = 120 cm³
- Answer: 120 cm³
Advanced Concepts and Problem-Solving Strategies
The maze might include more challenging problems involving:
- Combined shapes: Problems might require calculating the volume of a shape composed of multiple prisms or cylinders. This would involve calculating the volume of each component shape and then adding them together.
- Irregular shapes: Approximating the volume of irregularly shaped objects might involve using techniques like water displacement.
- Units of measurement: Pay close attention to the units used and ensure consistent units throughout your calculations.
Tips for Success in Solving Volume Problems
- Draw diagrams: Visualizing the problem with a diagram can significantly improve understanding.
- Break down complex shapes: Divide complex shapes into simpler components for easier calculation.
- Check your work: Always review your calculations to ensure accuracy.
- Use appropriate formulas: Select the correct formula based on the shape of the object.
- Practice: Consistent practice is key to mastering volume calculations.
This comprehensive guide provides a robust foundation for understanding and solving problems related to the volume of prisms and cylinders. Remember to practice regularly, utilize the strategies outlined, and always approach problems methodically. With diligent effort, you'll confidently navigate any maze—or real-world problem—that involves calculating volume.
Latest Posts
Latest Posts
-
Classify Each Molecule As An Aldehyde Ketone Or Neither
Mar 31, 2025
-
Ap Chem Unit 1 Progress Check Mcq
Mar 31, 2025
-
Student Exploration Coral Reefs 2 Biotic Factors Answer Key
Mar 31, 2025
-
The Accompanying Graph Represents The Supply Of Printer Ink Cartridges
Mar 31, 2025
-
Summary Of The First Chapter In To Kill A Mockingbird
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Volume Of Prisms And Cylinders Maze Answer Key . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
