Which Graph Represents Decreasing Distance With Increasing Time
Onlines
Apr 03, 2025 · 5 min read
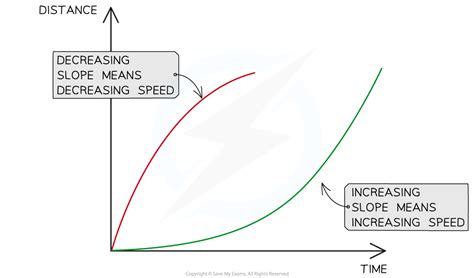
Table of Contents
Which Graph Represents Decreasing Distance with Increasing Time?
Understanding the relationship between distance and time is fundamental in various fields, from physics and mathematics to everyday life situations like tracking a journey. A common question that arises, especially in data analysis and interpreting graphs, is: "Which graph represents decreasing distance with increasing time?" This article will delve deep into this question, exploring different graph types, their interpretations, and real-world applications. We'll also touch upon the mathematical representation of this relationship and some common misconceptions.
Understanding the Concept of Decreasing Distance Over Time
Before we jump into the specifics of graph representation, let's solidify our understanding of the concept. Decreasing distance with increasing time implies that as time progresses, the distance from a reference point is getting smaller. This usually signifies a movement towards the reference point. Imagine driving back home from work; your distance from home decreases as your travel time increases until you finally reach home. This is the core idea we'll be visualizing graphically.
Graphical Representations: Identifying the Correct Graph
Several graph types can represent the relationship between distance and time. The most common and intuitive is a line graph, often called a distance-time graph. However, other types like scatter plots can also depict this relationship, albeit with different levels of precision and clarity. Let's focus on line graphs as the most appropriate method for this particular relationship.
The Decisive Indicator: Negative Slope
The key to identifying a graph representing decreasing distance over time lies in understanding the concept of slope. The slope of a line graph in a distance-time representation represents the speed or velocity of the object. A negative slope directly indicates a decreasing distance with increasing time.
A negative slope means that for every unit increase in time, there's a corresponding decrease in distance. This is the definitive characteristic of the graph we're seeking.
Consider a simple line graph:
- X-axis (Horizontal): Represents time (usually in seconds, minutes, hours, etc.)
- Y-axis (Vertical): Represents distance (usually in meters, kilometers, miles, etc.)
A straight line sloping downwards from left to right demonstrates a consistent decrease in distance over time. The steeper the slope, the faster the rate of decrease (i.e., faster speed towards the reference point).
Visualizing the Graph
Imagine a line starting at a high point on the Y-axis (representing an initial distance from the reference point). As the line moves to the right along the X-axis (representing increasing time), it should steadily descend towards the X-axis (representing decreasing distance). The point where the line intersects the X-axis represents the moment the object reaches the reference point (distance = 0).
Non-Linear Relationships
It's crucial to note that the relationship between distance and time doesn't always have to be linear. A curved line can also represent decreasing distance. For instance, if an object is slowing down as it approaches the reference point, the graph will show a curve that's initially steep (faster decrease) and gradually flattens (slower decrease) as it approaches the X-axis. However, even in non-linear cases, the essential characteristic remains: as time increases (movement to the right on the X-axis), distance decreases (movement downwards on the Y-axis).
Mathematical Representation
The mathematical relationship can be expressed in several ways depending on the nature of the decrease:
1. Linear Decrease:
This is the simplest case, represented by a linear equation of the form:
d = -vt + d₀
Where:
dis the distance at timetvis the constant speed (velocity) – note the negative sign indicating a decrease in distancetis the timed₀is the initial distance at time t=0
2. Non-linear Decrease:
Non-linear relationships require more complex functions. For example, a decreasing exponential function might represent a situation where the rate of decrease slows down over time. An example could be:
d = d₀ * e^(-kt)
Where:
kis a positive constant determining the rate of decay
Examples in Real-World Applications
Understanding graphs representing decreasing distance over time is crucial in various real-world scenarios:
- Tracking a vehicle: GPS systems constantly track the distance of a vehicle from a destination. The graph would show decreasing distance as the vehicle approaches.
- Monitoring a falling object: The distance of a falling object from the ground decreases with time until it hits the ground. The graph would visually represent this decrease.
- Analyzing a chemical reaction: In some chemical reactions, the concentration of a reactant decreases over time. A graph can visually represent this change.
- Monitoring the decay of a radioactive substance: The amount of radioactive material decreases over time. A graph would showcase this exponential decay.
- Tracking the progress of a journey: The distance to your destination will decrease as your travel time increases.
Common Misconceptions
One common misconception is confusing a decreasing distance-time graph with a constant speed graph. While a negative slope always indicates decreasing distance, it doesn't necessarily mean a constant speed. A curved line with a negative slope implies a varying speed (acceleration or deceleration). The slope at any point on the curve represents the instantaneous speed at that specific time.
Another misconception is interpreting the graph solely based on its shape. The crucial factor is the direction of the slope, not just the curve's shape. A downward-sloping line, whether straight or curved, represents decreasing distance.
Conclusion
Identifying the correct graph to represent decreasing distance with increasing time involves understanding the concept of slope in distance-time graphs. A negative slope, whether linear or non-linear, is the key indicator. This knowledge is vital in diverse fields for interpreting data, making predictions, and understanding the dynamics of various systems. By understanding this fundamental relationship and its graphical representation, we can gain valuable insights from data and apply this knowledge in numerous practical situations. Remember, the ultimate goal is to accurately visualize and interpret the relationship between distance and time to effectively communicate and analyze information.
Latest Posts
Latest Posts
-
Bacteria And Archaea Are Both Domains Consisting Of Prokaryotic Organisms
Apr 03, 2025
-
Blank Amplitudes Are Associated With Blank Sounds
Apr 03, 2025
-
The Break Even Point Is That Level Of Activity Where
Apr 03, 2025
-
Good Password Management Include Which Three Of The Following
Apr 03, 2025
-
Describe These People Using Expressions With Avoir
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Which Graph Represents Decreasing Distance With Increasing Time . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
