Right Triangles And Trigonometry Unit Test Part 1
Onlines
Apr 01, 2025 · 5 min read
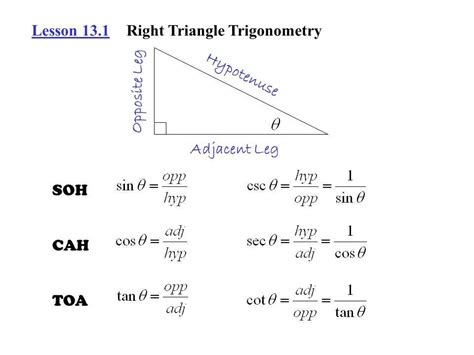
Table of Contents
Right Triangles and Trigonometry Unit Test Part 1: A Comprehensive Guide
This comprehensive guide will thoroughly prepare you for your right triangles and trigonometry unit test. We'll cover key concepts, essential formulas, problem-solving strategies, and practice problems to solidify your understanding. This is Part 1, focusing on the foundational aspects. Part 2 will delve into more advanced applications.
Understanding Right Triangles
A right triangle is a triangle with one angle measuring 90 degrees (a right angle). Understanding its properties is crucial for trigonometry. Let's review some key features:
- Hypotenuse: The side opposite the right angle. It's always the longest side in a right triangle.
- Legs (or Cathetus): The two sides that form the right angle. They are also known as the opposite and adjacent sides relative to a specific angle.
Pythagorean Theorem
The Pythagorean Theorem is a cornerstone of right triangle geometry. It states:
a² + b² = c²
where:
- 'a' and 'b' are the lengths of the legs.
- 'c' is the length of the hypotenuse.
This theorem allows us to calculate the length of one side if we know the lengths of the other two.
Example: If a = 3 and b = 4, then c² = 3² + 4² = 9 + 16 = 25, so c = 5.
Introduction to Trigonometry
Trigonometry deals with the relationships between angles and sides of triangles. In right-angled triangles, we use three primary trigonometric functions:
- Sine (sin): The ratio of the length of the side opposite an angle to the length of the hypotenuse. sin θ = opposite / hypotenuse
- Cosine (cos): The ratio of the length of the side adjacent to an angle to the length of the hypotenuse. cos θ = adjacent / hypotenuse
- Tangent (tan): The ratio of the length of the side opposite an angle to the length of the side adjacent to the angle. tan θ = opposite / adjacent
Understanding Angles and Sides
It's crucial to correctly identify the opposite, adjacent, and hypotenuse sides relative to the angle you're working with. The angle you're focusing on determines which side is opposite, adjacent, or the hypotenuse. Always draw a diagram to visualize the relationships.
Solving Right Triangles
Solving a right triangle means finding the lengths of all its sides and the measures of all its angles. Here's a step-by-step approach:
- Identify what you know: Note the given information – sides and/or angles.
- Choose the appropriate trigonometric function: Based on the given information and what you need to find, select the relevant trigonometric function (sin, cos, or tan).
- Set up the equation: Write the equation using the chosen trigonometric function and the known values.
- Solve for the unknown: Use algebraic manipulation to solve for the unknown side or angle.
- Check your answer: Verify your solution using the Pythagorean theorem or other trigonometric identities.
Example Problems
Let's work through some examples to solidify our understanding:
Example 1: Finding a side length
A right triangle has a hypotenuse of length 10 and one leg of length 6. Find the length of the other leg.
- Solution: We can use the Pythagorean theorem: a² + b² = c². Let a = 6 and c = 10. Then 6² + b² = 10², so b² = 100 - 36 = 64, and b = 8.
Example 2: Finding an angle
A right triangle has legs of length 5 and 12. Find the measure of the angle opposite the leg of length 12.
- Solution: We can use the tangent function: tan θ = opposite / adjacent = 12/5. Therefore, θ = arctan(12/5) ≈ 67.4 degrees.
Example 3: Using multiple trigonometric functions
In a right triangle, angle A is 30 degrees, and the hypotenuse is 20 cm. Find the lengths of the sides opposite and adjacent to angle A.
- Solution:
- Opposite side: sin 30° = opposite / 20. Since sin 30° = 0.5, the opposite side = 20 * 0.5 = 10 cm.
- Adjacent side: cos 30° = adjacent / 20. Since cos 30° ≈ 0.866, the adjacent side ≈ 20 * 0.866 ≈ 17.32 cm.
Special Right Triangles
Certain right triangles have special angle and side relationships that simplify calculations. These are:
- 45-45-90 triangle: This isosceles right triangle has two 45-degree angles and side ratios of 1:1:√2.
- 30-60-90 triangle: This triangle has angles of 30, 60, and 90 degrees, with side ratios of 1:√3:2.
Knowing these ratios can significantly speed up problem-solving.
Inverse Trigonometric Functions
Inverse trigonometric functions (arcsin, arccos, arctan) are used to find the angle when you know the ratio of sides. For example, if sin θ = 0.5, then θ = arcsin(0.5) = 30 degrees. Calculators are essential for computing these values.
Remember to set your calculator to the correct angle mode (degrees or radians) depending on the problem's requirements.
Angles of Elevation and Depression
These concepts often appear in word problems involving right triangles.
- Angle of elevation: The angle between the horizontal and the line of sight when looking upward at an object.
- Angle of depression: The angle between the horizontal and the line of sight when looking downward at an object.
Remember that the angle of elevation and the angle of depression are equal when observing the same object from different locations.
Practice Problems
Here are some practice problems to test your understanding:
-
A ladder 15 meters long leans against a wall. The base of the ladder is 9 meters from the wall. How high up the wall does the ladder reach?
-
A plane takes off at an angle of elevation of 15 degrees. After traveling 500 meters, what is the plane's altitude?
-
From the top of a lighthouse 50 meters tall, the angle of depression to a boat is 30 degrees. How far is the boat from the base of the lighthouse?
-
A right triangle has a hypotenuse of 10 and one angle of 45 degrees. Find the lengths of the other sides.
-
A triangle has sides of length 7, 24, and 25. Is it a right triangle? Explain.
Solving these problems will reinforce the concepts covered and prepare you for your unit test. Remember to consistently practice and review the material to achieve mastery. Good luck! This concludes Part 1. Part 2 will cover more advanced topics and problem types.
Latest Posts
Latest Posts
-
Assisted Living Can Be Thought Of As A Combination Of
Apr 03, 2025
-
12 1 Identifying The Substance Of Genes
Apr 03, 2025
-
25 3 11 Packet Tracer Logging From Multiple Sources
Apr 03, 2025
-
Which Graph Represents Decreasing Distance With Increasing Time
Apr 03, 2025
-
The Lone Ranger And Tonto Fistfight In Heaven Analysis
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Right Triangles And Trigonometry Unit Test Part 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
