Which Of The Following Segments Is A Diameter Of 0
Onlines
Apr 05, 2025 · 4 min read
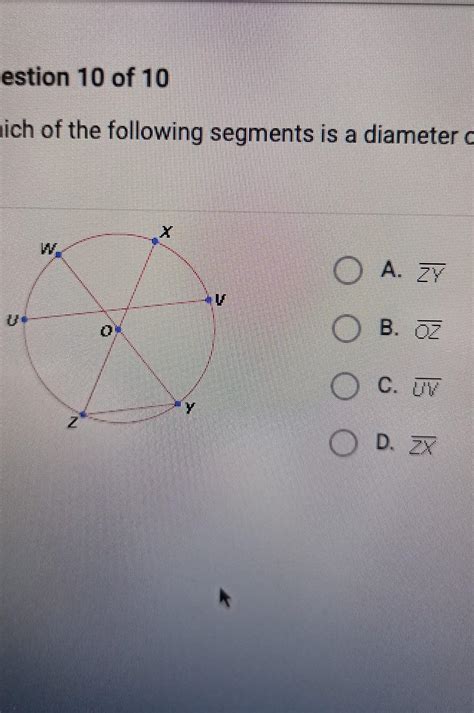
Table of Contents
Which of the Following Segments is a Diameter of 0? Understanding Diameters and Their Properties
The question, "Which of the following segments is a diameter of 0?" requires a nuanced understanding of geometric concepts, specifically diameters and their relationship to circles and other shapes. A diameter of zero presents a unique case, pushing the boundaries of our typical understanding of circles and prompting an exploration of limiting cases and the mathematical implications. Let's delve into this fascinating topic.
Understanding Diameters
Before we tackle the question of a zero-diameter segment, let's establish a firm foundation in the definition and properties of diameters.
A diameter is a straight line segment that passes through the center of a circle and whose endpoints lie on the circle. It's the longest chord of a circle and is precisely twice the length of the radius. The radius, in turn, is the distance from the center of a circle to any point on the circle.
Key Properties of Diameters:
- Length: The length of the diameter is twice the length of the radius (Diameter = 2 * Radius).
- Center: The diameter passes through the center of the circle.
- Longest Chord: The diameter is the longest chord in a circle.
- Symmetry: A diameter divides the circle into two congruent semicircles.
- Perpendicular Bisector: Any diameter is a perpendicular bisector of all chords that are perpendicular to it.
The Concept of a Zero-Diameter Segment
The idea of a diameter with a length of zero immediately challenges our intuitive understanding of circles. A circle, as typically defined, requires a non-zero radius. A circle with a radius of zero is, in essence, a single point. This single point has no dimension, and therefore, it cannot contain a line segment, let alone a diameter. Consequently, a segment with a length of zero cannot be considered a diameter in the traditional sense.
Mathematical Implications
From a mathematical perspective, a zero-diameter segment represents a degenerate case. Degenerate cases often arise in mathematics when the conditions defining a shape or concept are pushed to their limits. In this case, the circle degenerates into a single point. While the term "diameter" is typically associated with a circle with a positive radius, this mathematical subtlety can be analyzed within different frameworks.
Exploring Related Concepts
To further understand the implications of a zero-diameter, let's explore some related geometric concepts:
- Circles with vanishingly small radii: Imagine a sequence of circles with progressively smaller radii, approaching zero. As the radius approaches zero, the diameter also approaches zero. This sequence of circles converges to a single point.
- Limits and Continuity: The concept of a zero-diameter can be explored using the language of limits and continuity. We can consider a function that maps the radius of a circle to its diameter. This function is continuous, and as the radius approaches zero, the diameter also approaches zero. This concept is fundamental in calculus.
- Point as a Degenerate Circle: Consider a point as a degenerate case of a circle. While it doesn't fit the typical definition of a circle, it's a logical consequence of shrinking the radius to zero. This highlights the need to consider boundary conditions in geometry.
Analyzing the Question: Which Segment is a Diameter of 0?
Given the above discussion, the answer to the question "Which of the following segments is a diameter of 0?" depends heavily on the context and the definition of a "diameter" being employed.
If we strictly adhere to the standard definition of a diameter as a line segment passing through the center of a circle with its endpoints on the circle, then none of the segments can be a diameter of 0. This is because a diameter must have a positive length. A zero-length segment is simply a point, and a point doesn't satisfy the requirements of a diameter.
However, if we consider the degenerate case of a circle reduced to a single point, we could argue that the "segment" consisting of that single point might be considered a degenerate diameter of 0. This is not a standard interpretation, but a way of thinking about limiting cases in geometry.
Context is Key
The interpretation of a zero-diameter segment heavily relies on context. Different mathematical fields may handle degenerate cases differently. A rigorous understanding of the underlying mathematical definitions is crucial for correctly interpreting such situations.
Conclusion
The question of a zero-diameter segment presents a fascinating exploration of the boundaries of geometric concepts. While a zero-length segment cannot be a diameter in the traditional sense because it cannot be part of a circle, exploring the limiting cases allows us to develop a richer understanding of circles, their properties, and the nuances of mathematical definitions. The concept of a degenerate case, as seen with the zero-diameter, illuminates the importance of considering boundary conditions and their mathematical interpretations within different frameworks. Ultimately, correctly interpreting such questions requires a thorough understanding of geometric definitions and the context in which they are applied. The key takeaway is that precision in language and a firm grasp of mathematical principles are crucial for navigating such seemingly simple yet conceptually rich problems.
Latest Posts
Latest Posts
-
The Core Mechanisms Of Group Process And Change Include
Apr 05, 2025
-
How Old To Work At Dennys
Apr 05, 2025
-
Which Data Type Stores Only One Of Two Values
Apr 05, 2025
-
Activity 11 1 Structural Drawings For A Commercial Building Project
Apr 05, 2025
-
5 3 Application Problem Accounting Answers
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Segments Is A Diameter Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
