Which Sequence Of Transformations Carries Abcd Onto Efgh
Onlines
Mar 26, 2025 · 6 min read
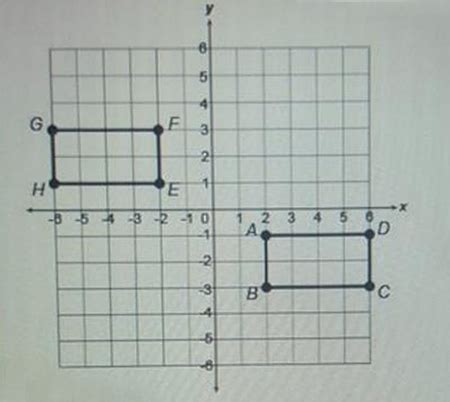
Table of Contents
Which Sequence of Transformations Carries ABCD onto EFGH? A Comprehensive Guide
Determining the sequence of transformations that map one quadrilateral onto another is a fundamental concept in geometry. This process involves analyzing the relationships between corresponding vertices, sides, and angles of the two shapes. While seemingly straightforward, the challenge lies in identifying the specific transformations – translation, rotation, reflection, or dilation – and their order to achieve the perfect mapping. This article will provide a comprehensive guide to solving such problems, covering various scenarios and offering practical strategies.
Understanding the Basic Transformations
Before diving into complex scenarios, it's crucial to understand the four fundamental geometric transformations:
1. Translation
A translation involves moving a shape a certain distance in a specific direction. It doesn't change the shape's size or orientation. It's defined by a translation vector, which indicates the horizontal and vertical shift.
2. Rotation
Rotation involves turning a shape around a fixed point (the center of rotation) by a specific angle. The shape's size remains unchanged, but its orientation alters. The description of a rotation includes the center of rotation and the angle of rotation (clockwise or counterclockwise).
3. Reflection
Reflection involves mirroring a shape across a line (the line of reflection). The reflected shape is a mirror image of the original, with the same size and shape but reversed orientation.
4. Dilation
Dilation involves enlarging or reducing a shape by a specific scale factor. The shape's orientation remains the same, but its size changes proportionally. A scale factor greater than 1 indicates enlargement, while a scale factor between 0 and 1 indicates reduction.
Strategies for Identifying Transformation Sequences
Determining the sequence of transformations requires a systematic approach. Here's a step-by-step strategy:
1. Analyze Corresponding Vertices
Begin by identifying corresponding vertices between the two quadrilaterals (ABCD and EFGH). This means finding which vertex in EFGH corresponds to each vertex in ABCD. This is often the most crucial first step. Label your vertices clearly.
2. Check for Congruence or Similarity
Determine if the quadrilaterals are congruent (same size and shape) or similar (same shape, different size).
-
Congruence: If the quadrilaterals are congruent, the transformations involved will only be translation, rotation, and/or reflection. Dilation is not necessary.
-
Similarity: If the quadrilaterals are similar, dilation will be one of the transformations involved, along with potentially translation, rotation, and/or reflection.
3. Identify the Transformations in Sequence
This is the most challenging step and requires careful observation and reasoning. There might be multiple valid sequences, but the goal is to find the most efficient and logical one. Consider the following:
-
Start with Translation: Often, it's easiest to start by considering translation. See if translating ABCD brings it closer to aligning with EFGH. If so, find the translation vector required to achieve this partial alignment.
-
Rotation: After translation, look for rotational alignment. Does rotating ABCD around a specific point bring it even closer to aligning with EFGH? Determine the center and angle of rotation required.
-
Reflection: Once translation and rotation are considered, look for the need for reflection. If the shapes are oriented in opposite directions despite translation and rotation, a reflection is likely required. Identify the line of reflection.
-
Dilation: If the shapes are similar but not congruent, a dilation is necessary. Determine the scale factor and center of dilation. Note that the order of dilation relative to other transformations can significantly impact the final result. Experiment to find what order works best.
4. Verify the Sequence
Once you have identified a potential sequence of transformations, verify it by applying the transformations step-by-step to ABCD. If the transformed ABCD precisely overlaps with EFGH, your sequence is correct.
Example Scenarios and Solutions
Let's consider a few examples to illustrate these strategies. Note that due to the limitations of text-based media, visualizing these transformations would be best done with interactive geometry software. However, we will describe the process thoroughly.
Scenario 1: Congruent Quadrilaterals
Suppose quadrilateral ABCD has vertices A(1,1), B(3,1), C(4,3), D(2,3) and quadrilateral EFGH has vertices E(5,4), F(7,4), G(8,6), H(6,6).
-
Analysis: The quadrilaterals appear to be congruent.
-
Translation: Translating ABCD by the vector <4,3> maps A to (5,4), which coincides with E.
-
Verification: Applying the same translation to B, C, and D aligns them perfectly with F, G, and H respectively.
Solution: A single translation by the vector <4,3> maps ABCD onto EFGH.
Scenario 2: Similar Quadrilaterals
Let's consider another example. Quadrilateral ABCD has vertices A(1,1), B(2,1), C(2,2), D(1,2). Quadrilateral EFGH has vertices E(3,3), F(6,3), G(6,6), D(3,6).
-
Analysis: These quadrilaterals are similar, but not congruent. EFGH is larger than ABCD.
-
Dilation: A dilation centered at the origin with a scale factor of 3 will enlarge ABCD. Applying this dilation gives A'(3,3), B'(6,3), C'(6,6), D'(3,6).
Solution: A dilation centered at the origin with a scale factor of 3 maps ABCD onto EFGH.
Scenario 3: Requiring Multiple Transformations
Consider a more complex case where ABCD requires multiple transformations. This scenario illustrates the importance of a systematic approach. Let's say ABCD needs a translation, rotation, and reflection. Imagine a situation where, after translation and rotation, the image is a mirror image of EFGH. In this case, the reflection would be the final step. The precise coordinates and the sequence would depend on the specific locations of the vertices.
Advanced Considerations and Challenges
-
Multiple Valid Sequences: In some cases, multiple sequences of transformations can map one quadrilateral onto another. For instance, a combination of translation, rotation, and reflection might be equivalent to a different combination involving dilation and rotation. The most efficient and logical sequence is usually preferred.
-
Non-linear Transformations: This article focuses on linear transformations (translation, rotation, reflection, dilation). More complex transformations exist, but they are beyond the scope of this introductory guide.
-
Using Technology: Interactive geometry software can be invaluable for visualizing and experimenting with transformations. This allows for a more intuitive understanding and faster solution finding.
Conclusion
Determining the sequence of transformations that map one quadrilateral onto another is a valuable skill in geometry. By systematically analyzing the relationships between corresponding vertices, understanding the basic transformations, and following a logical step-by-step approach, you can effectively solve these problems. Remember that practice and the use of appropriate tools, like interactive geometry software, can significantly enhance your ability to master this geometric concept. Remember to always verify your solution to ensure accuracy. This comprehensive guide provides a solid foundation for tackling various scenarios with confidence.
Latest Posts
Latest Posts
-
Match The Windows 10 Registry Key With Its Description
Mar 29, 2025
-
Draw The Correct Product For The Given Diels Alder Reaction
Mar 29, 2025
-
Which Of The Following Is The Empirical Formula For C12h18o6
Mar 29, 2025
-
Which Element Of Endgame Helps Establish The Idea Of Circularity
Mar 29, 2025
-
Symbolism In Dr Jekyll And Mr Hyde
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Which Sequence Of Transformations Carries Abcd Onto Efgh . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
